Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной.
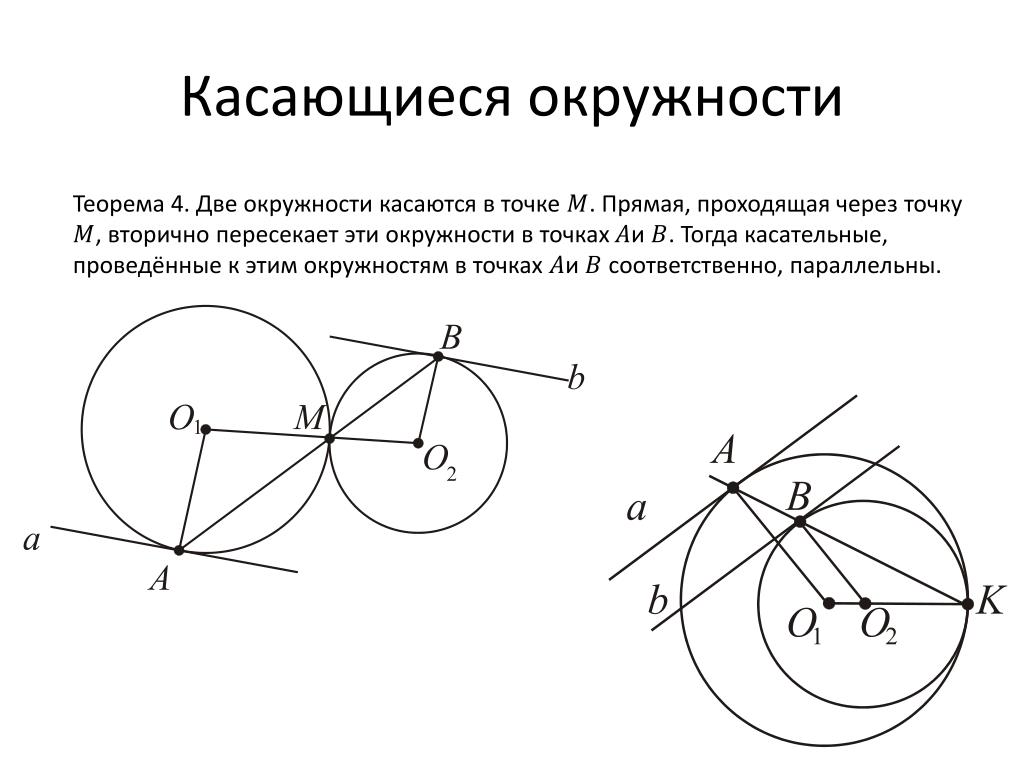
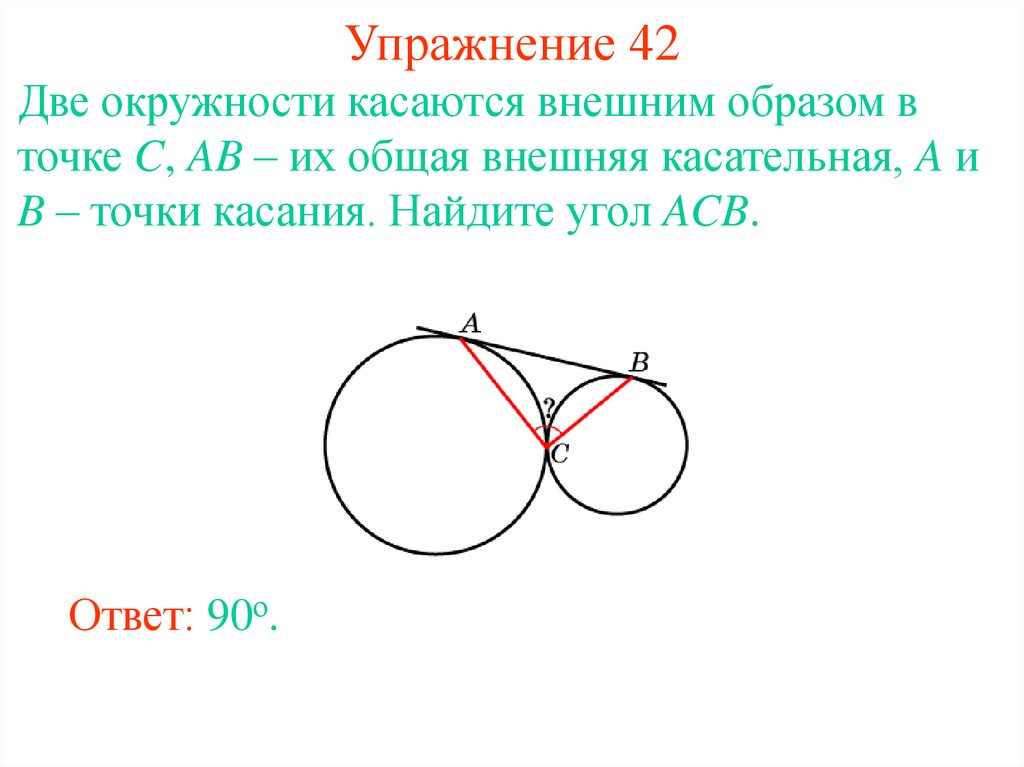Если две окружности с разными радиусами касаются внешним образом, то их центры и точка касания лежат на биссектрисе угла, образованного общими внешними касательными.
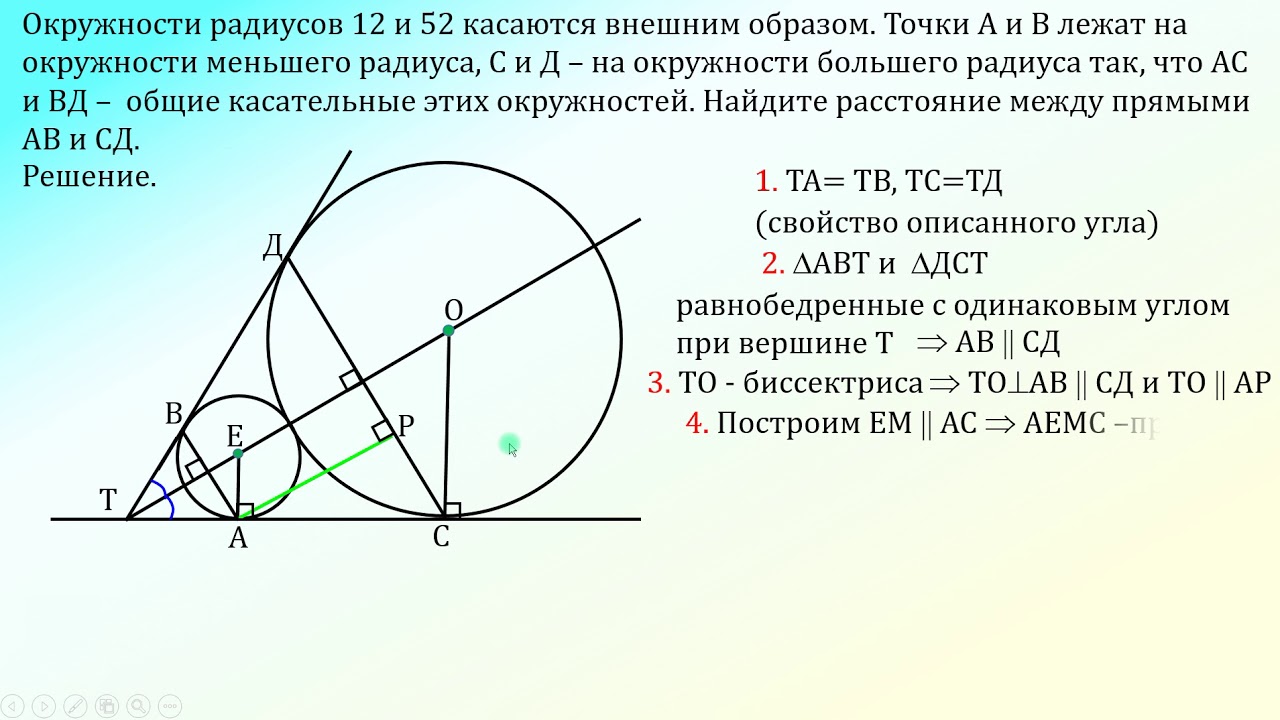
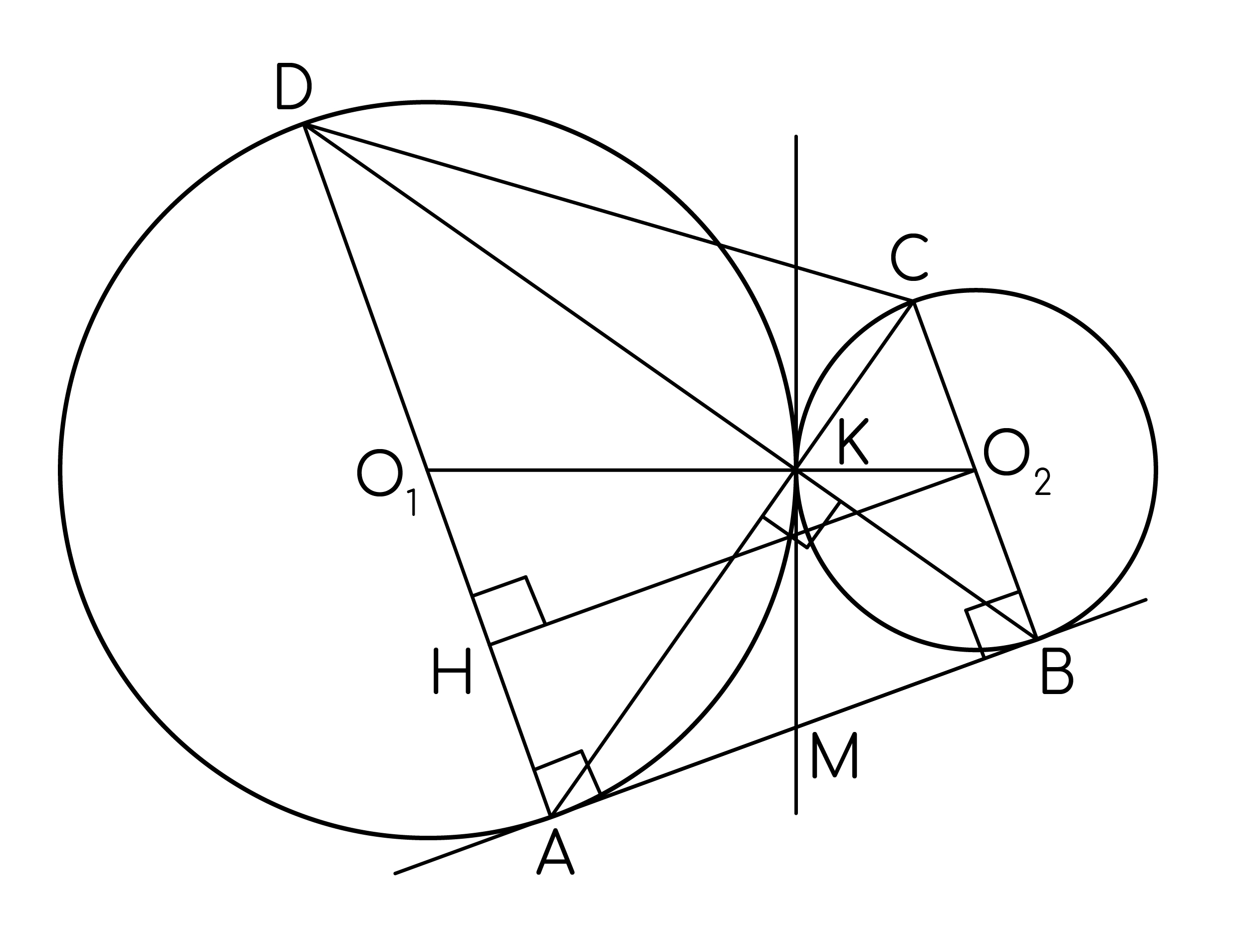
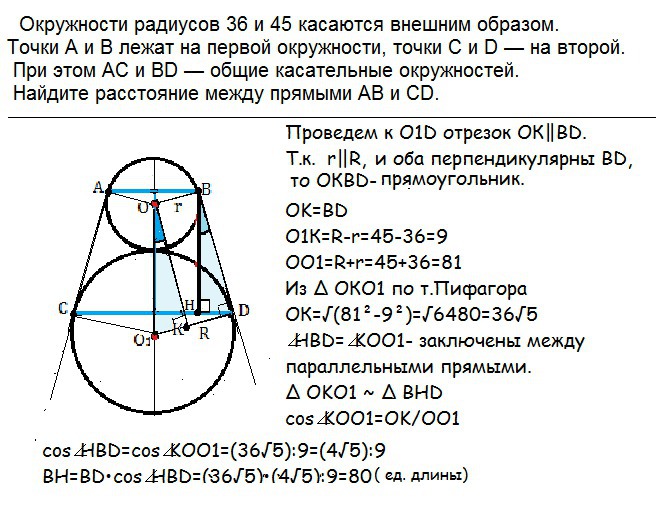
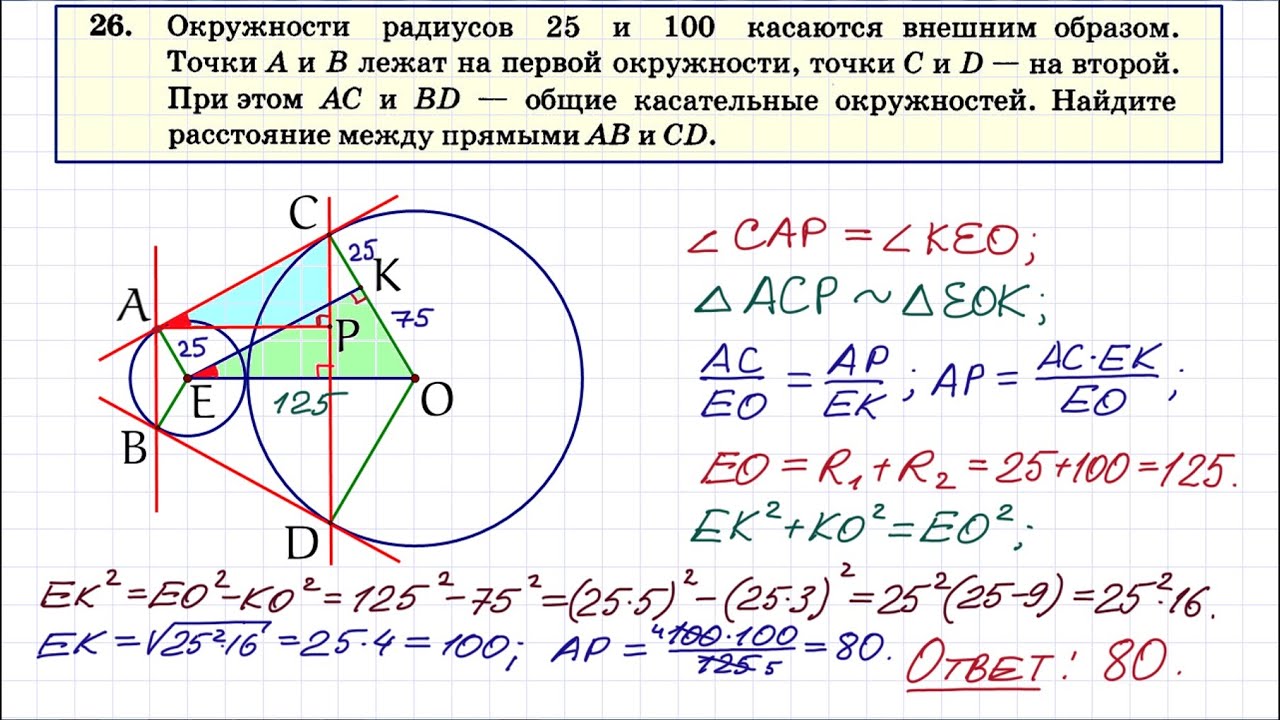
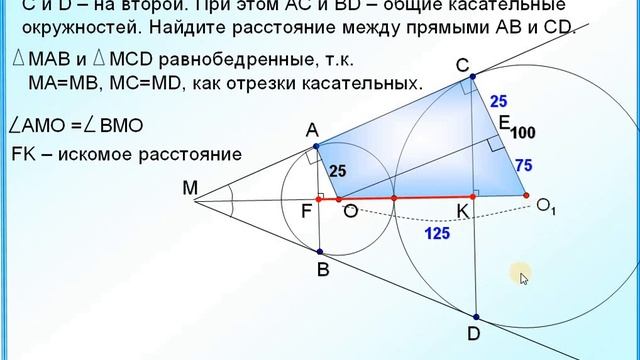
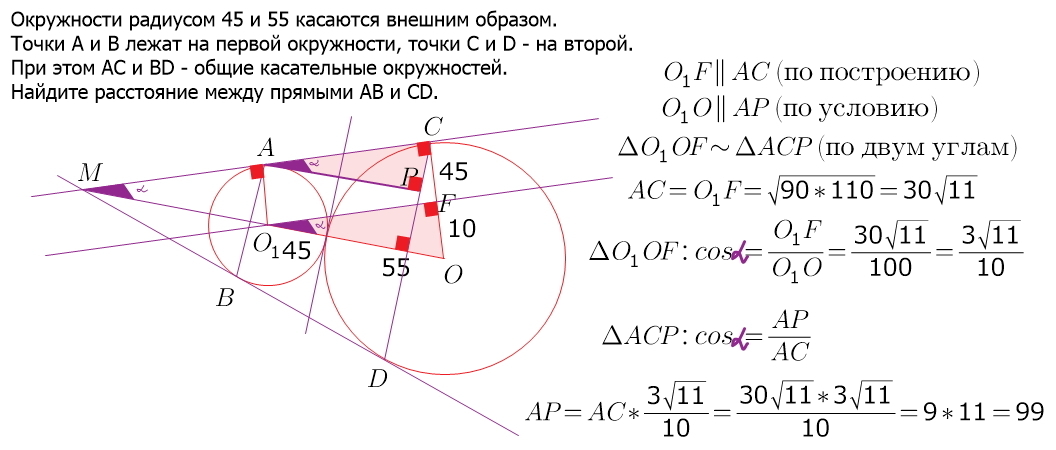Окружности радиусов 14 и 35 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные …
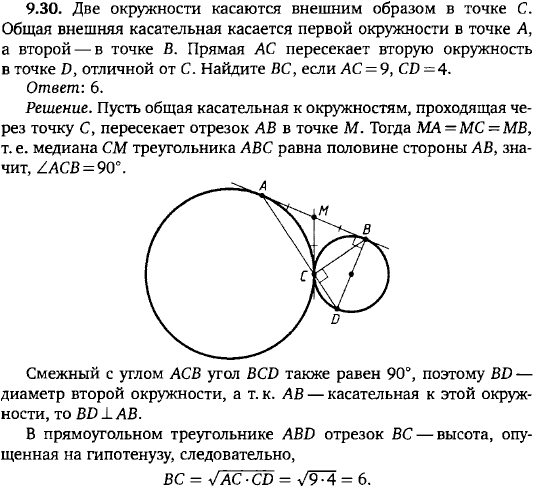
Если две окружности касаются внешним образом, то хорды, соединяющие точку касания этих окружностей с точками касания окружностей с их общей внешней касательной, пересекаются под прямым углом: Внешне …
Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов.
Построенные окружности имеют только одну общую точку c. Говорят, что они касаются внешним образом. При внешнем касании двух окружностей, расстояние между их …
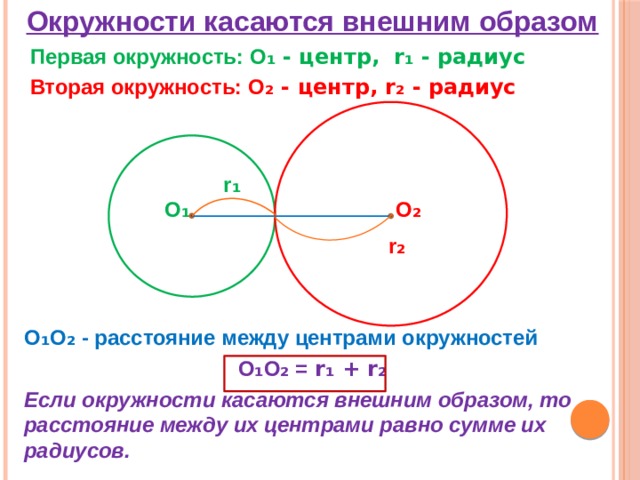
Когда две окружности касаются друг друга внешним образом, их центры находятся на одной прямой, проходящей через точку касания. Расстояние между …
Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной. Внутреннее касание …
Общую касательную к двум окружностям называют внешней, если обе окружности лежат по одну сторону от этой касательной, так на рисунке 4 прямые n 1 k 1 и n 2 k 2 - внешние касательные окружностей.
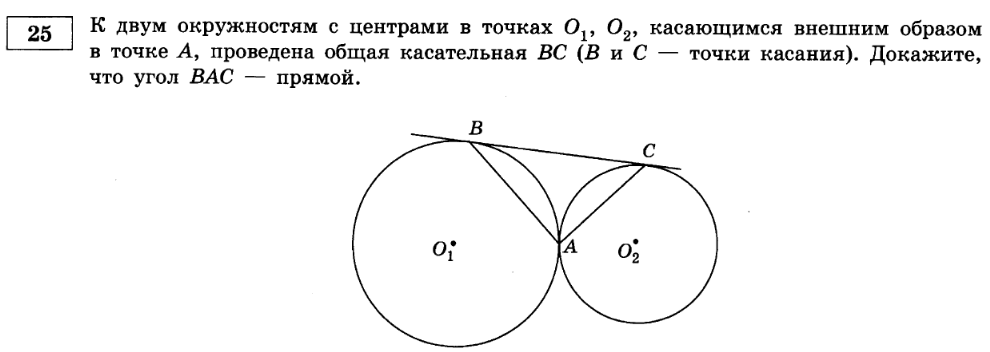Касание окружностей может быть внешним и внутренним. Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны …
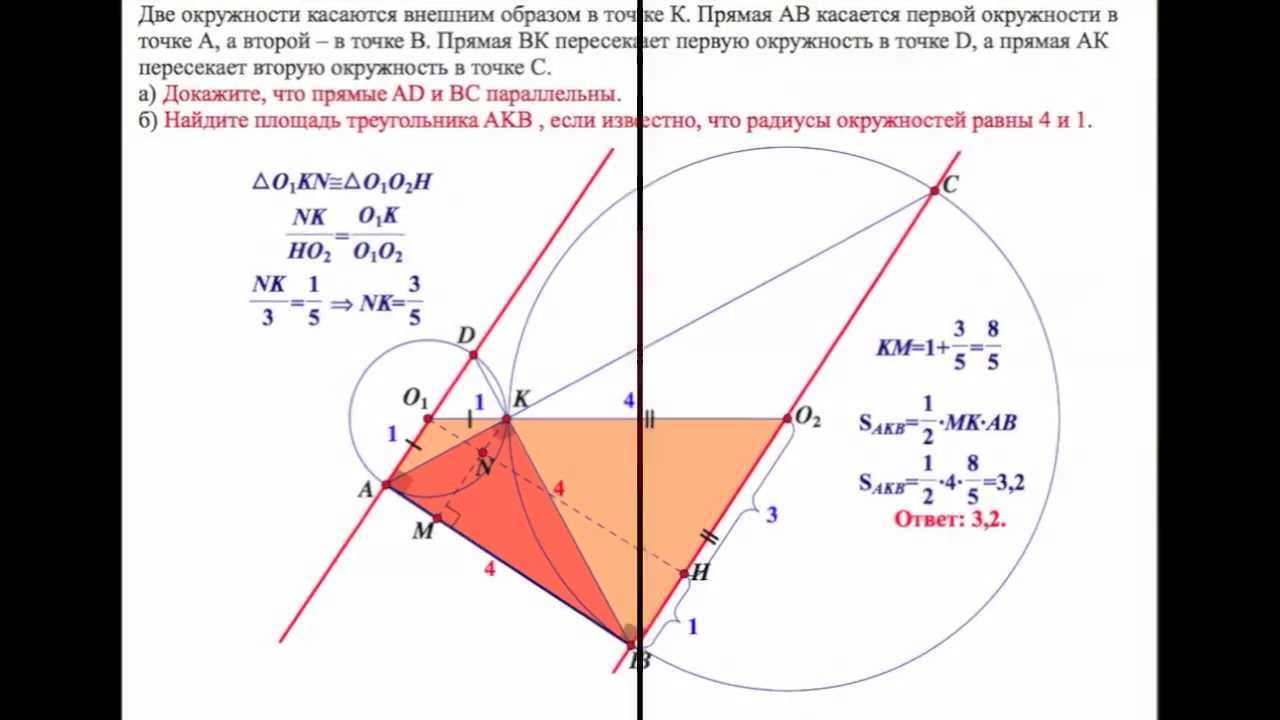
Если две окружности касаются внешне, то отрезки общих касательных равны между собой: Где: a, b – общие касательные окружностей; c – общая внешняя касательная; А и В – точки касания окружностей с прямой a; C и …
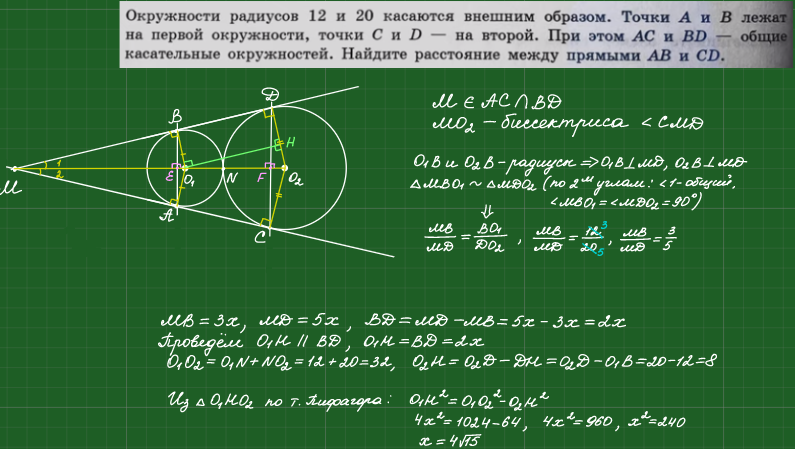Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные …
при внешнем касании: OO1 = R + r; при внутреннем касании: OO1 = R − r. Касательные к окружности. Определения и основная теорема. Прямая касается окружности, если …
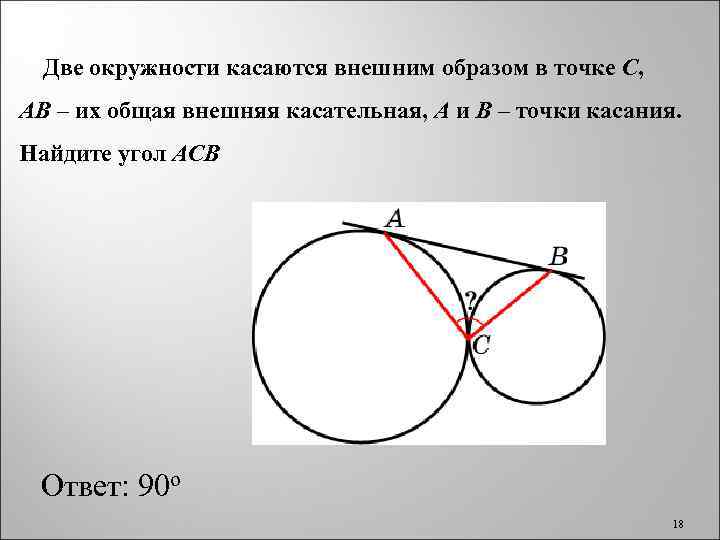Окружности касаются внешним образом, если они расположены вне друг друга. Пусть \(R_1\) и \(R_2\) – радиусы окружностей \(\omega_1\) и \(\omega_2\) и \(d\) – расстояние …
Окружности, касающиеся внешним образом, — это особый тип геометрических фигур. Они касаются друг друга в точке снаружи каждой окружности, …
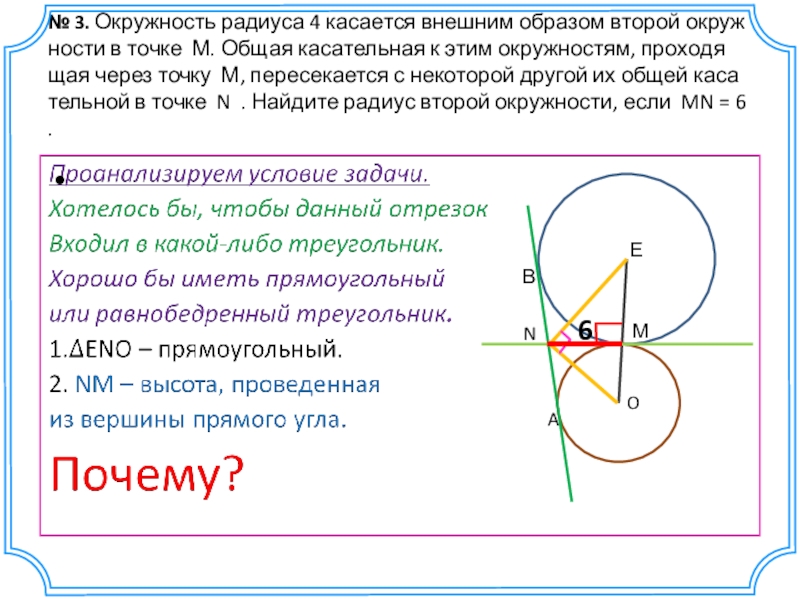
Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов: Длина …
Еще по теме:
Еще по теме:
