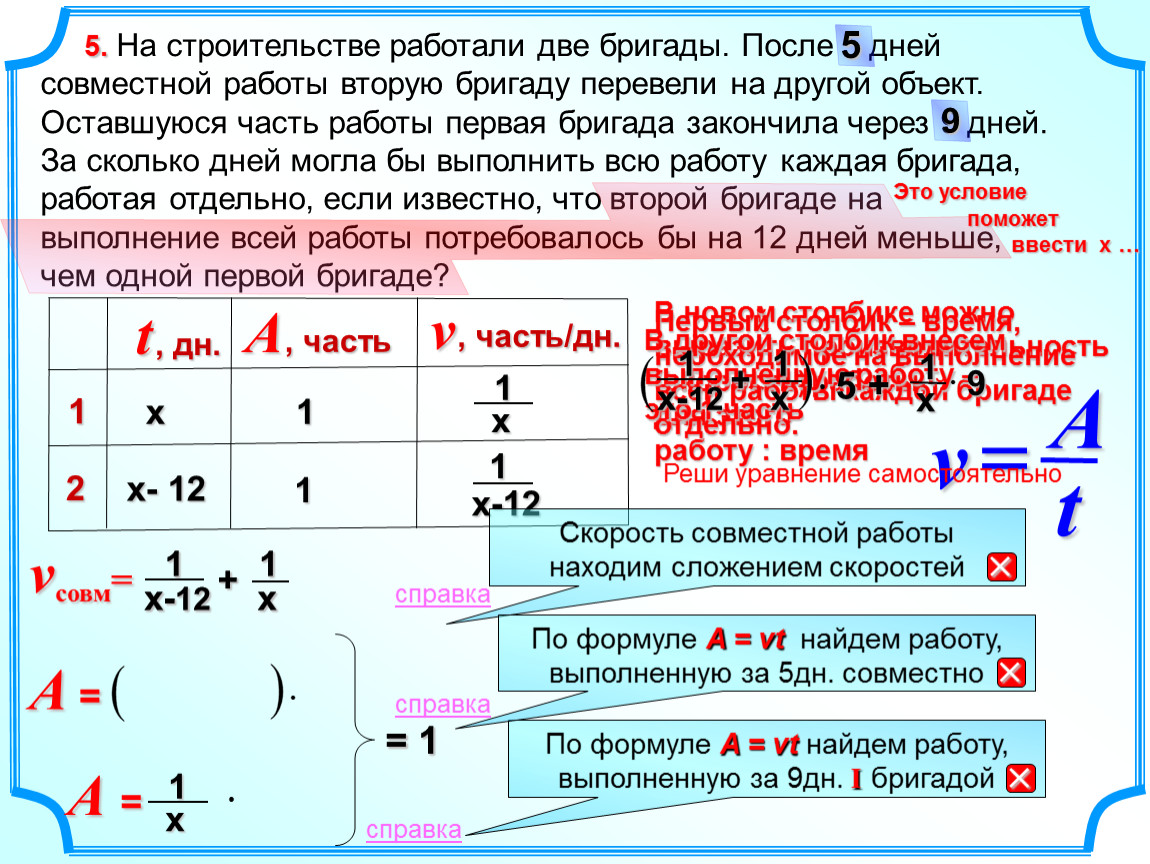
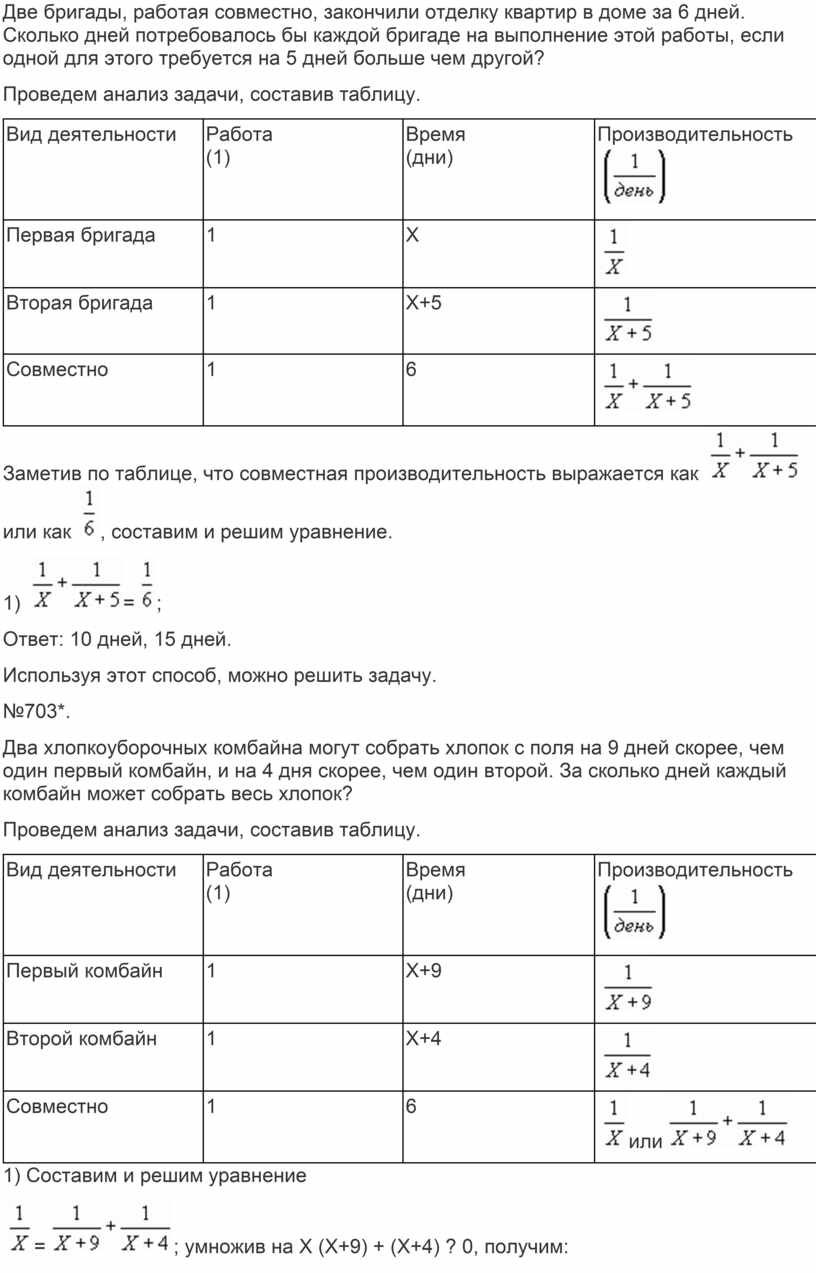
Две бригады, работая вместе, могут выполнить производственное задание за 8 дней. Если первая бригада, работая самостоятельно, выполнит 1/3 задания, а затем её.
Подробный ответ из решебника (ГДЗ) на Номер 7.22 по учебнику А.Г. Мордкович и др. Задачник по алгебре 7 класса. Часть 2. 12 издание, Мнемозина, 2010г.
Две бригады, работая вместе, могут выполнить задание за 8 ч. Первая бригада, работая одна, могла бы выполнить задание на 12 ч быстрее, чем вторая бригада.
Две бригады, работая вместе, могут выполнить производственное задание за 8 дней. Если первая бригада, работая самостоятельно, выполнит 1/3 задания, а затем ее сменит …
Ответы. Аркадий 5 лет назад. Примем выполняемую работу за единицу. Пусть первая бригада выполняет эту работу за: Х ч. При этом Х > 0. Скорость работы первой бригады …
За сколько часов это задание выполнят две бригады при совместной работе? Решение: Примем всю работу за единицу, тогда за 1 час первая бригада выполняет, а вторая. …
Две бригады, работая вместе, вспахали поле за \( \displaystyle 6\) часов. За сколько часов может вспахать поле первая бригада, работая самостоятельно, если ей необходимо на \( \displaystyle 5\) часов меньше.
За сколько часов может вспахать поле каждая бригада, работая самостоятельно, если одной бригаде на это потребуется на 12 ч больше, чем другой?
Ответы 1. Ефим 6 лет назад. Примем за x и y времена выполнения работы каждой бригадой по отдельности, тогда: 1 : x = 1/x - производительность труда первой бригады; 1 : y = 1/y - …
Две бригады, работая вместе, выполняют работу за 6 ч. Одной первой бригаде на ту же работу требуется на 5 ч больше, чем второй. За какое время может выполнить всю.
2 бригада всю работу выполняет за у часов за 1 час - 1/у часть работы. за 9 часов вместе 9/х+9/у=1. 2/3 первой бригады за 12 часов выполняет 12*2/3х=8/х. 4/5 второй бригады за …
Первая бригада выполнит работу (примем ее объем за единицу) за u часов, вторая бригада - за v часов: v = u + 12; 8(1/u + 1/v) = 1.
Пусть первая бригада одна вылоняет задание за t часов, тогда вторая - за (t+12). Если вся работа равна 1. то работая вместа, за час они делают (1/t+1/(t+12)).
Решение #1. Рассмотрим вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 8 класс, Просвещение: 486. Две бригады строителей, работая вместе, …
Две бригады, работая вместе, могут отремонтировать дорогу за 20 дней. Первая бригада работала на ремонте дороги 9 дней, после чего к ней присоединилась вторая.
Две бригады, работая вместе, вспахали поле за 8 часов. За какое время может вспахать поле каждая бригадая, работая самостоятельно, если второй бригаде потребуется на 12 …
Еще по теме:
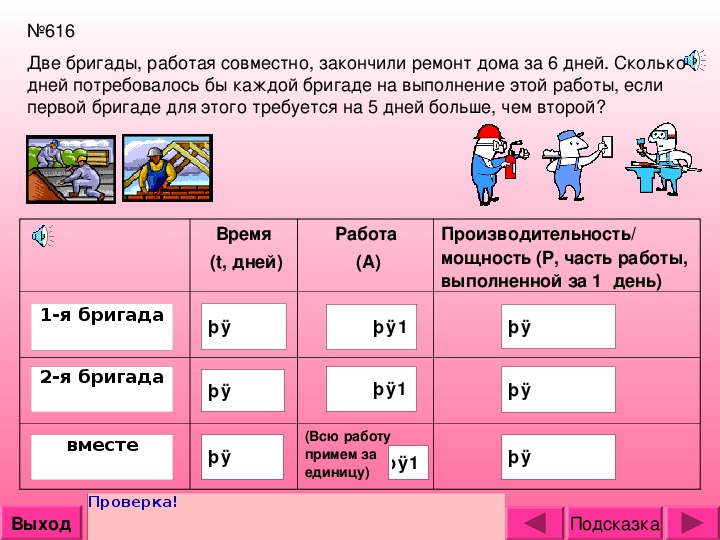
Еще по теме:
