Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк?
Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк?
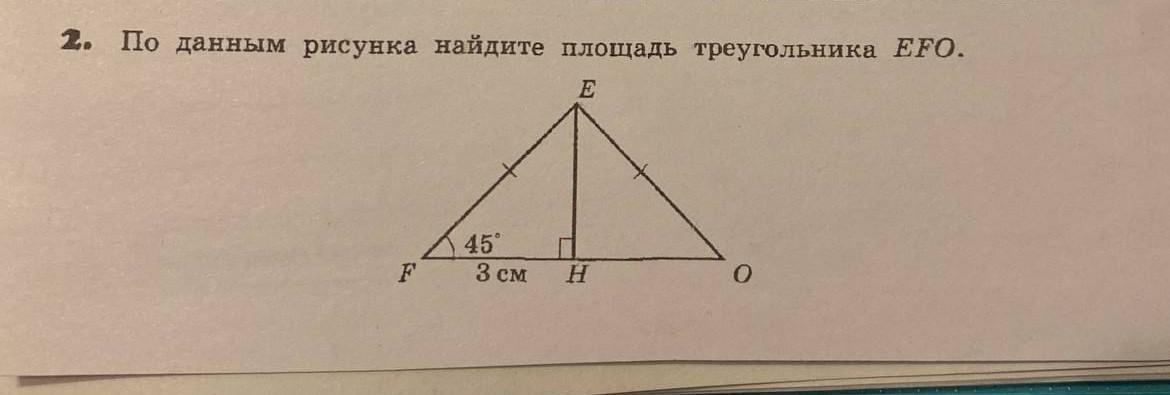
 Эта формула позволяет найти площадь треугольника, используя длины высот, опущенных на стороны треугольника. Формула полупроизведения высот: S = 0.5 * h₁ * h₂ * h₃,
Эта формула позволяет найти площадь треугольника, используя длины высот, опущенных на стороны треугольника. Формула полупроизведения высот: S = 0.5 * h₁ * h₂ * h₃,
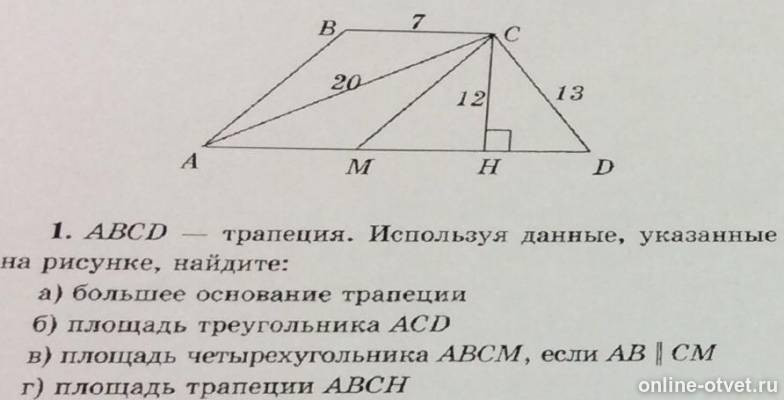
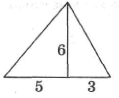
 Площадь треугольника = высота*сторона, к которой она проведена/2. Сторона, к которой проведена высота = 5+8=13. Площадь = 13*6/2 = 13*3 = 39.
Площадь треугольника = высота*сторона, к которой она проведена/2. Сторона, к которой проведена высота = 5+8=13. Площадь = 13*6/2 = 13*3 = 39.
 На рисунке дан треугольник со сторонами ab, bc и ac. Шаг 1: Проверим, есть ли необходимые данные для нахождения площади треугольника. Длины сторон …
На рисунке дан треугольник со сторонами ab, bc и ac. Шаг 1: Проверим, есть ли необходимые данные для нахождения площади треугольника. Длины сторон …
 Пользователь Анна Власова задал вопрос в категории Другие предметы и получил на него 1 ответ
Пользователь Анна Власова задал вопрос в категории Другие предметы и получил на него 1 ответ
 Формула площади треугольника S=1/2h*a, где a — сторона, к которой опущена высота, h — высота S= 1/2*6*(5+3)=24
Формула площади треугольника S=1/2h*a, где a — сторона, к которой опущена высота, h — высота S= 1/2*6*(5+3)=24
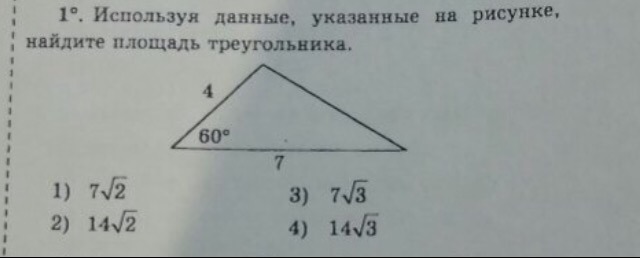
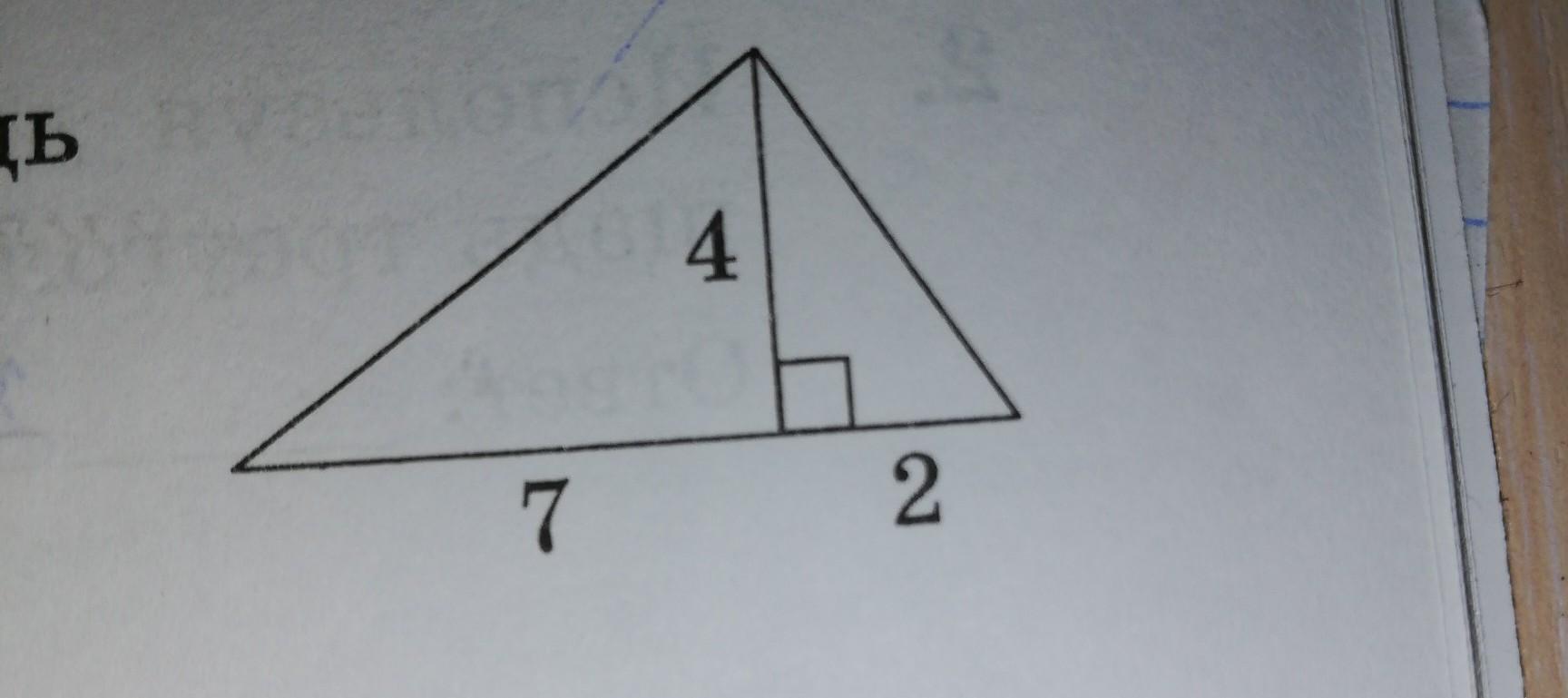
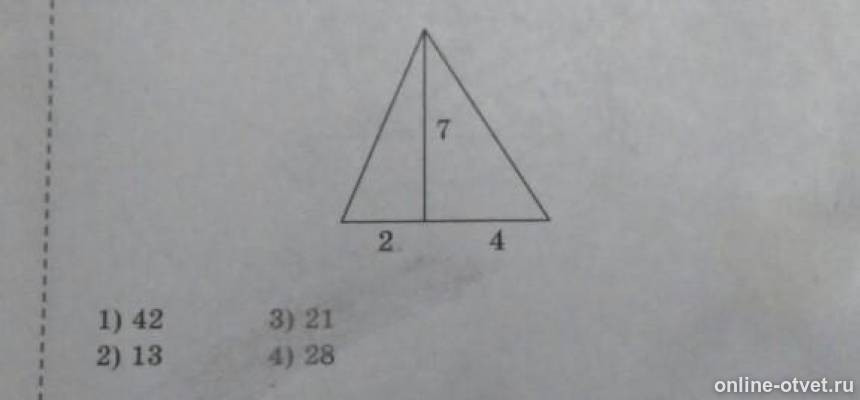
 площадь треугольника ровна 1/2 основания на высоту , 1/2(4+2)*7=21
площадь треугольника ровна 1/2 основания на высоту , 1/2(4+2)*7=21
 Где S — площадь треугольника, p — полупериметр треугольника (p = (a + b + c) / 2), а a, b и c — длины сторон треугольника. Подставив значения сторон треугольника в формулу …
Где S — площадь треугольника, p — полупериметр треугольника (p = (a + b + c) / 2), а a, b и c — длины сторон треугольника. Подставив значения сторон треугольника в формулу …
 cкачать: Домашнее задание "Площадь треугольника" 8 класс. Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, …
cкачать: Домашнее задание "Площадь треугольника" 8 класс. Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, …
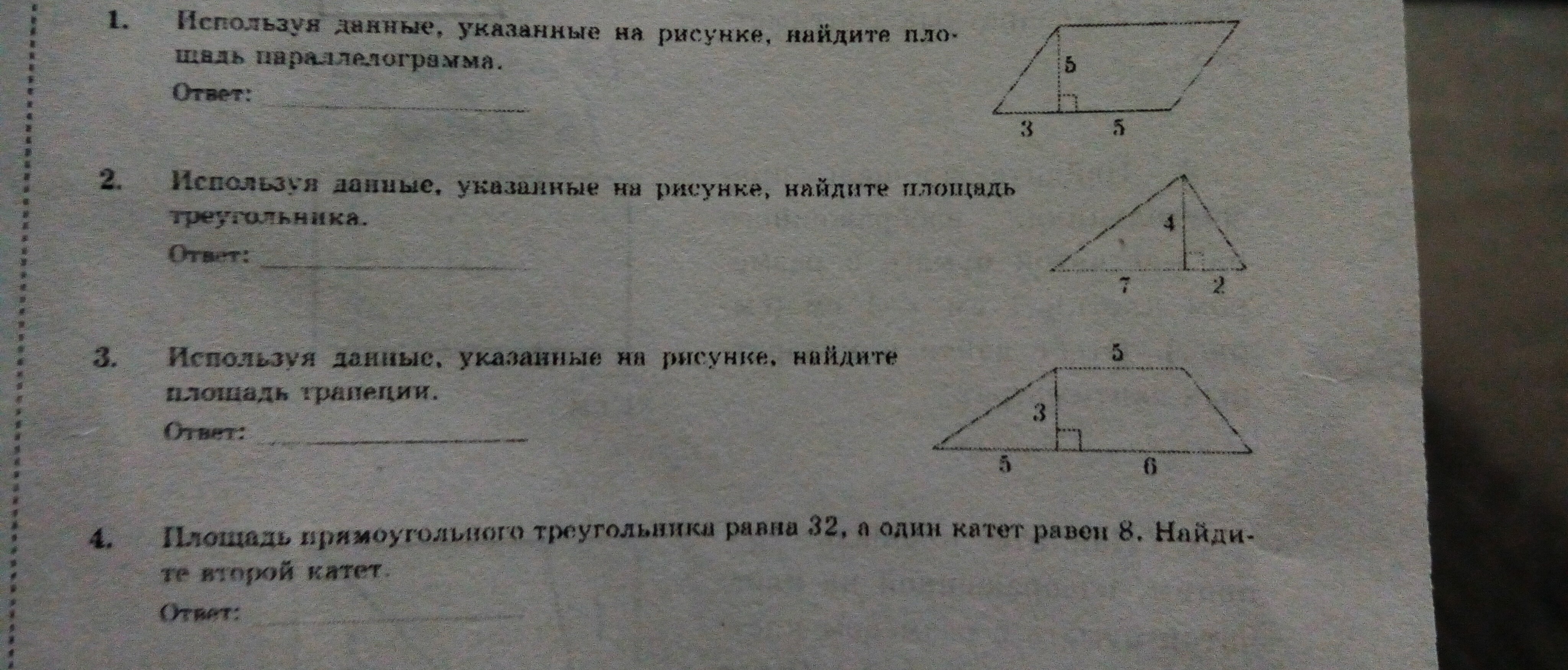 Для начала, вспомним, что площадь треугольника можно вычислить по формуле: S = (a * h) / 2, где «a» — длина основания треугольника, а «h» — высота, опущенная на это …
Для начала, вспомним, что площадь треугольника можно вычислить по формуле: S = (a * h) / 2, где «a» — длина основания треугольника, а «h» — высота, опущенная на это …
 Пользователь Арсений Сафонов задал вопрос в категории Другие предметы и получил на него 2 ответа
Пользователь Арсений Сафонов задал вопрос в категории Другие предметы и получил на него 2 ответа
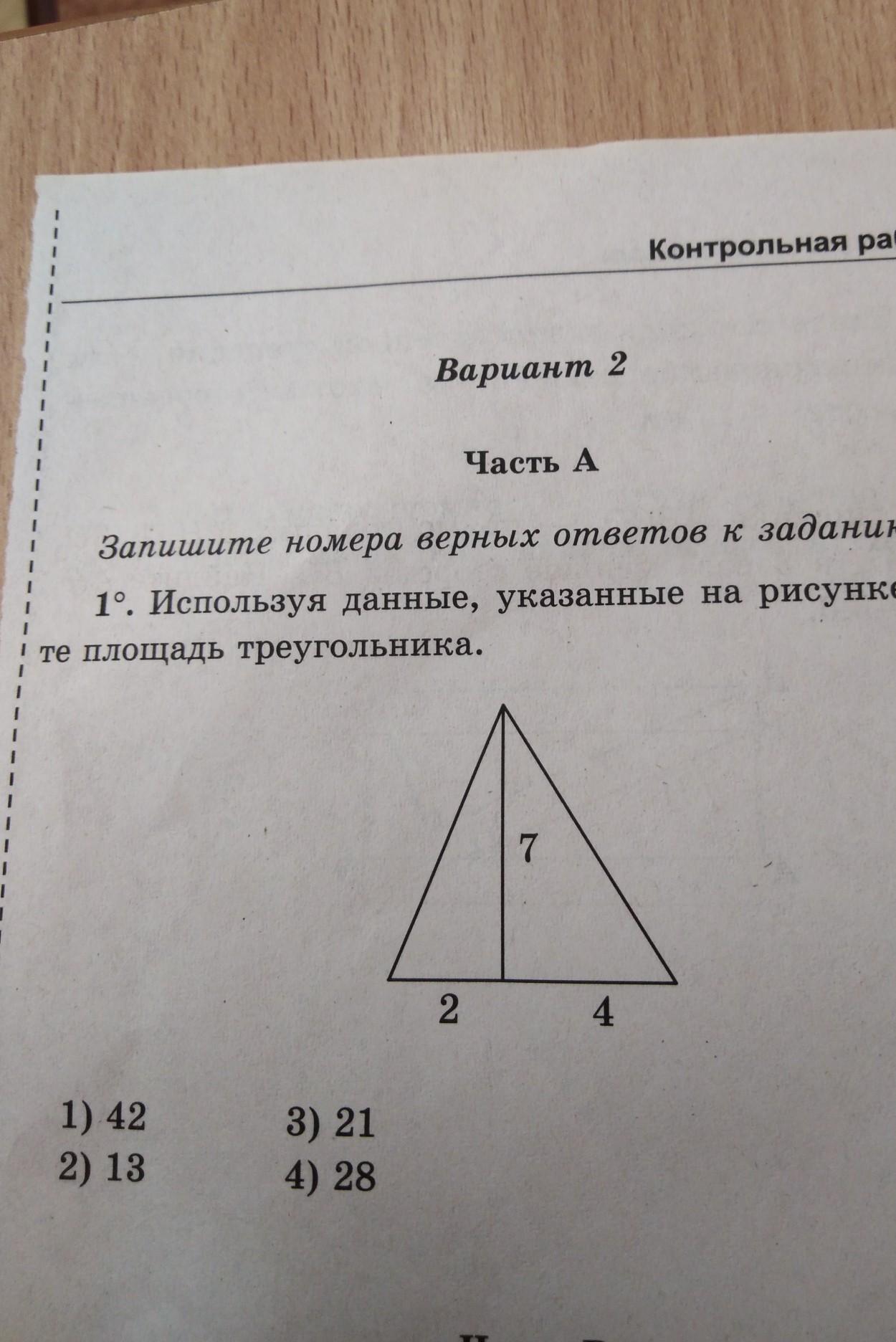 Используя данные. указанные на рисунке найдите площадь треугольника Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Используя данные. указанные на рисунке найдите площадь треугольника Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
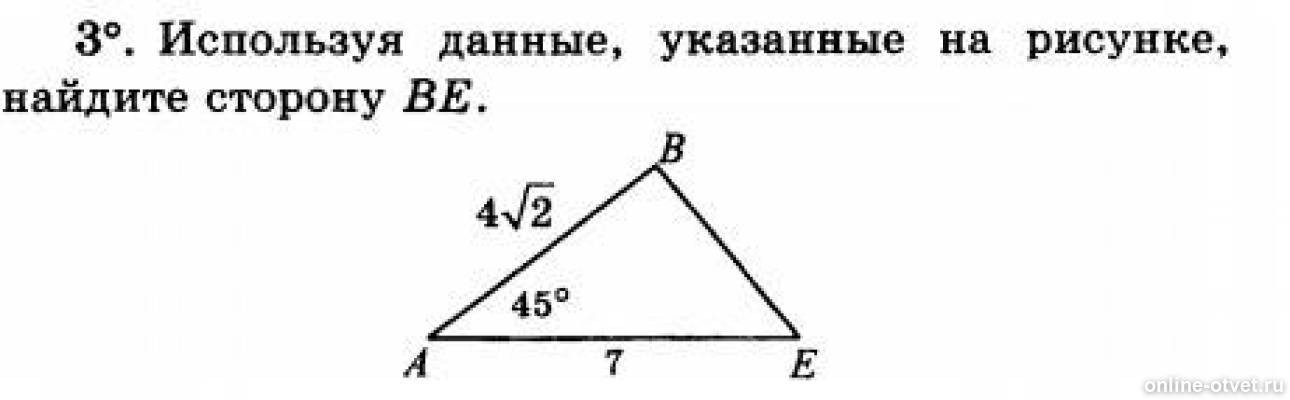
 С помощью трафарета, катет напротив в 30 градусов равен половине гипотенузе, т.е 2. А высота, т.е. катет напротив в 60 градусов, равен 2^3. Тогда по формуле площади …
С помощью трафарета, катет напротив в 30 градусов равен половине гипотенузе, т.е 2. А высота, т.е. катет напротив в 60 градусов, равен 2^3. Тогда по формуле площади …
 Проведем высоту ВН,следов. угол АНВ=90,из этого угол АВН=30,АН=2(катет лежащий против угла в 30 градусов равен половине гипотинузы) ВН=х х^2*2^2=4^2(х в квадрате …
Проведем высоту ВН,следов. угол АНВ=90,из этого угол АВН=30,АН=2(катет лежащий против угла в 30 градусов равен половине гипотинузы) ВН=х х^2*2^2=4^2(х в квадрате …
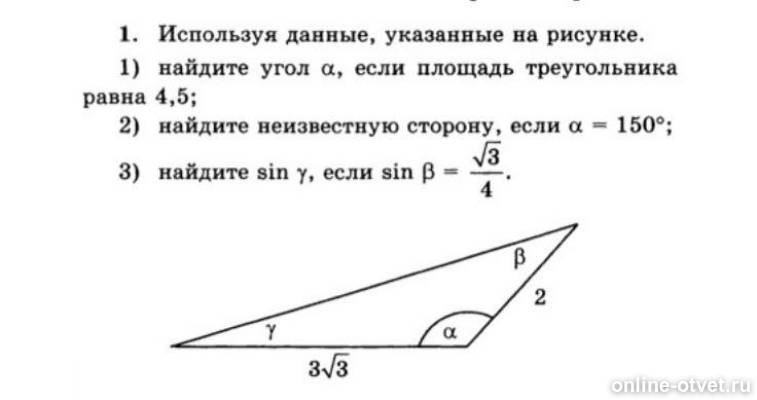
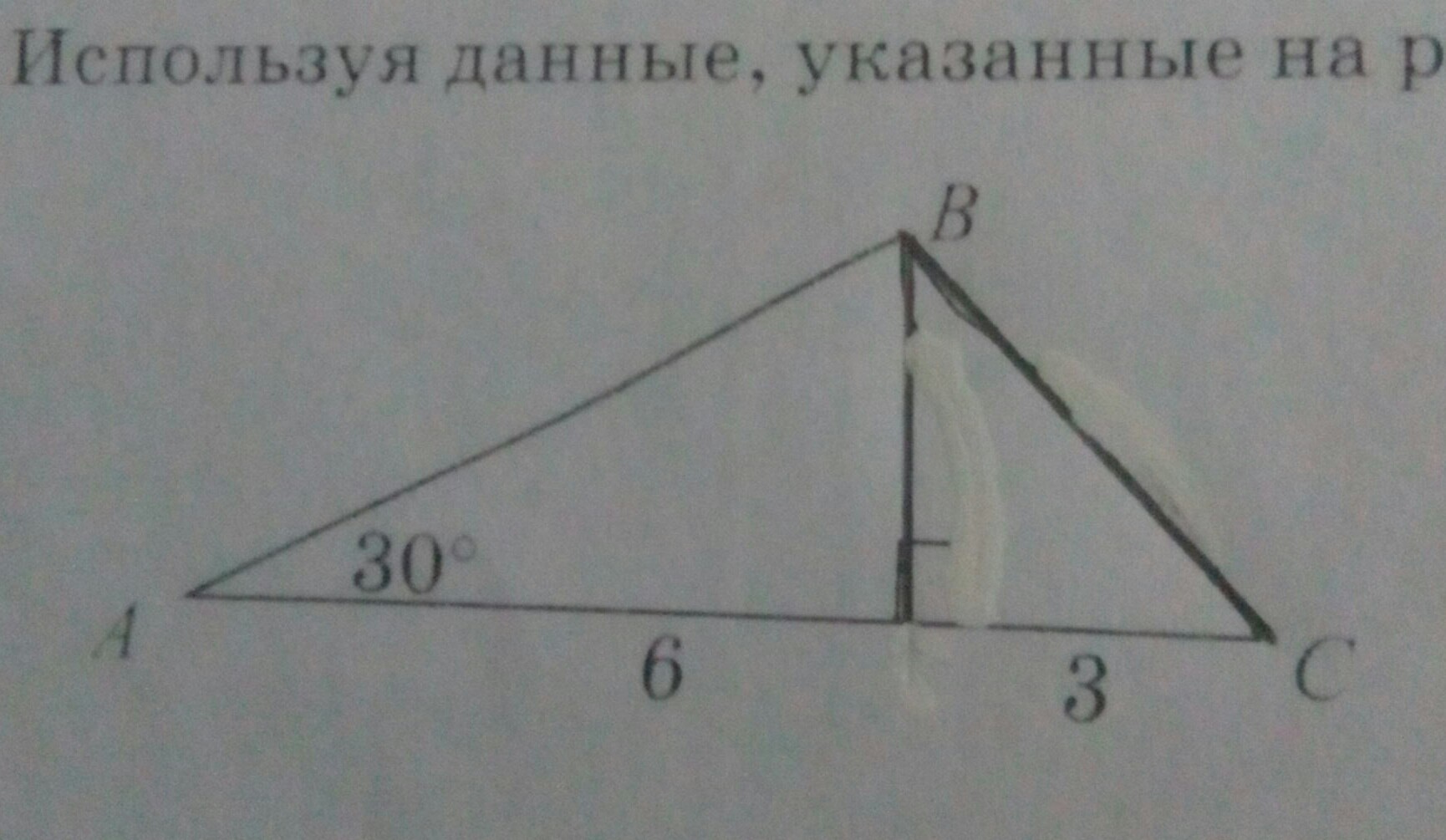 Для решения задачи нам требуется знать значения двух сторон треугольника и значение угла между этими сторонами.
Для решения задачи нам требуется знать значения двух сторон треугольника и значение угла между этими сторонами.
 Используя данные, указанные на рисунке, найдите площадь треугольника. Одна сторона 4, основание - 7 угол между ними 60 градусов.
Используя данные, указанные на рисунке, найдите площадь треугольника. Одна сторона 4, основание - 7 угол между ними 60 градусов.
Еще по теме:











Еще по теме: