 Свойство 1: произведение степеней. При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели …
Свойство 1: произведение степеней. При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели …
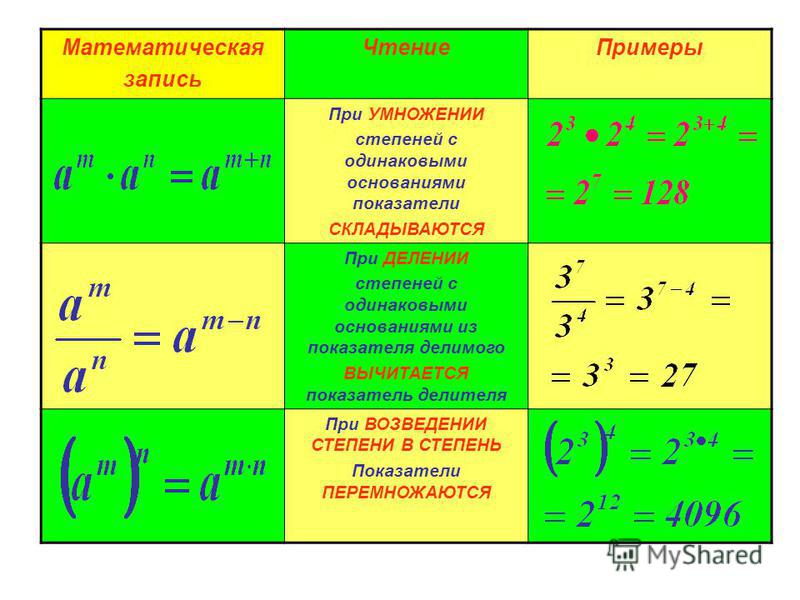
 Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней. Так, a 2.a 6 = a 2+6 = a 8. И x 3.x 2.x = x 3+2+1 = x 6. Или: 4a n ⋅ 2a …
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней. Так, a 2.a 6 = a 2+6 = a 8. И x 3.x 2.x = x 3+2+1 = x 6. Или: 4a n ⋅ 2a …
 Свойства степеней и действия с ними: основные формулы, примеры решения задач на деление и умножение, сложение и вычитание степеней с одинаковыми и …
Свойства степеней и действия с ними: основные формулы, примеры решения задач на деление и умножение, сложение и вычитание степеней с одинаковыми и …

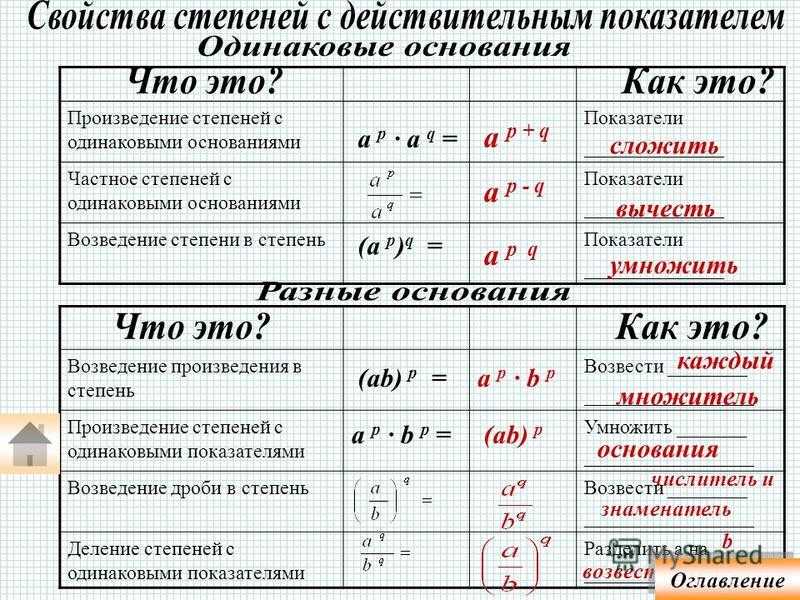
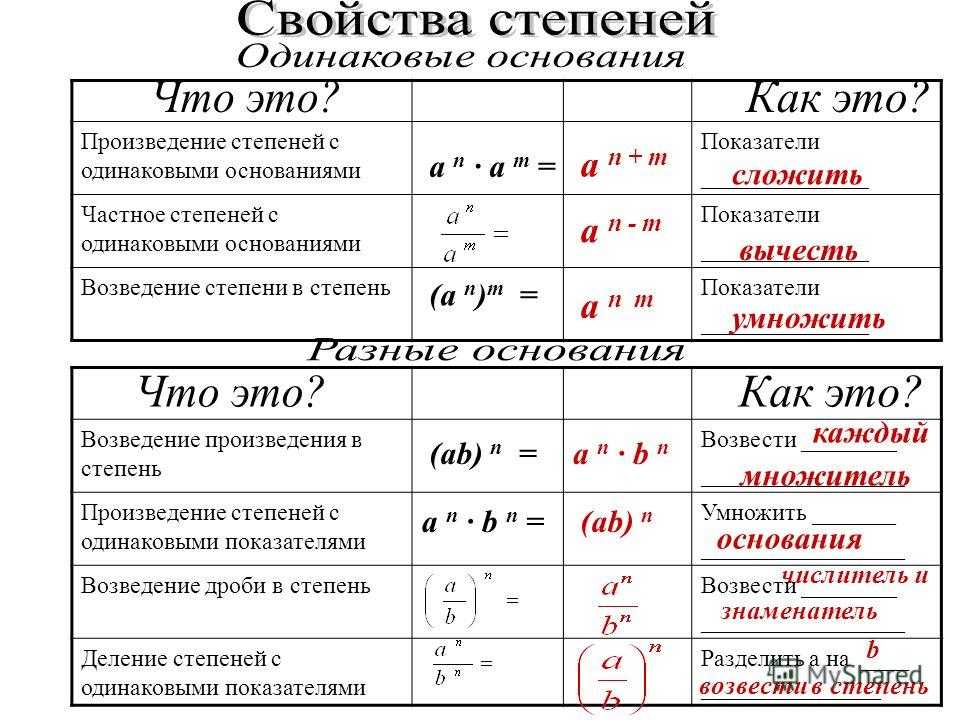
 Умножение степеней с одинаковыми основаниями. Степени с одинаковыми основаниями умножаются путём сложения показателей степеней: a m · a n = a m+n, где. a — …
Умножение степеней с одинаковыми основаниями. Степени с одинаковыми основаниями умножаются путём сложения показателей степеней: a m · a n = a m+n, где. a — …
 Правило 1: При вычитании степеней с одинаковыми основаниями вычитаемые показатели вычитаются неизменно. Например: 4 3 — 4 2 = 4 1. Правило 2: Если степени имеют …
Правило 1: При вычитании степеней с одинаковыми основаниями вычитаемые показатели вычитаются неизменно. Например: 4 3 — 4 2 = 4 1. Правило 2: Если степени имеют …
 Деление степеней с одинаковым основанием. Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с …
Деление степеней с одинаковым основанием. Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с …
 Рассмотрим выражение, в котором a≠0 (так как на нуль делить нельзя) и m>n (если m≤n, то получим число в целой степени, а мы рассматриваем доказательство для натуральных …
Рассмотрим выражение, в котором a≠0 (так как на нуль делить нельзя) и m>n (если m≤n, то получим число в целой степени, а мы рассматриваем доказательство для натуральных …
 если перемножаем два числа с одинаковыми основаниями и разными степенями, то основание остаётся, а степени складываются. Если эти же числа делят - то степени вычитаются.
если перемножаем два числа с одинаковыми основаниями и разными степенями, то основание остаётся, а степени складываются. Если эти же числа делят - то степени вычитаются.
 В алгебре найти произведение степеней можно в двух случаях: 1) если степени имеют одинаковые основания; 2) если степени имеют одинаковые показатели.
В алгебре найти произведение степеней можно в двух случаях: 1) если степени имеют одинаковые основания; 2) если степени имеют одинаковые показатели.
 Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует. Запишем эти свойства-правила в виде формул: a m × a n = a m+n. a m ÷ a n …
Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует. Запишем эти свойства-правила в виде формул: a m × a n = a m+n. a m ÷ a n …
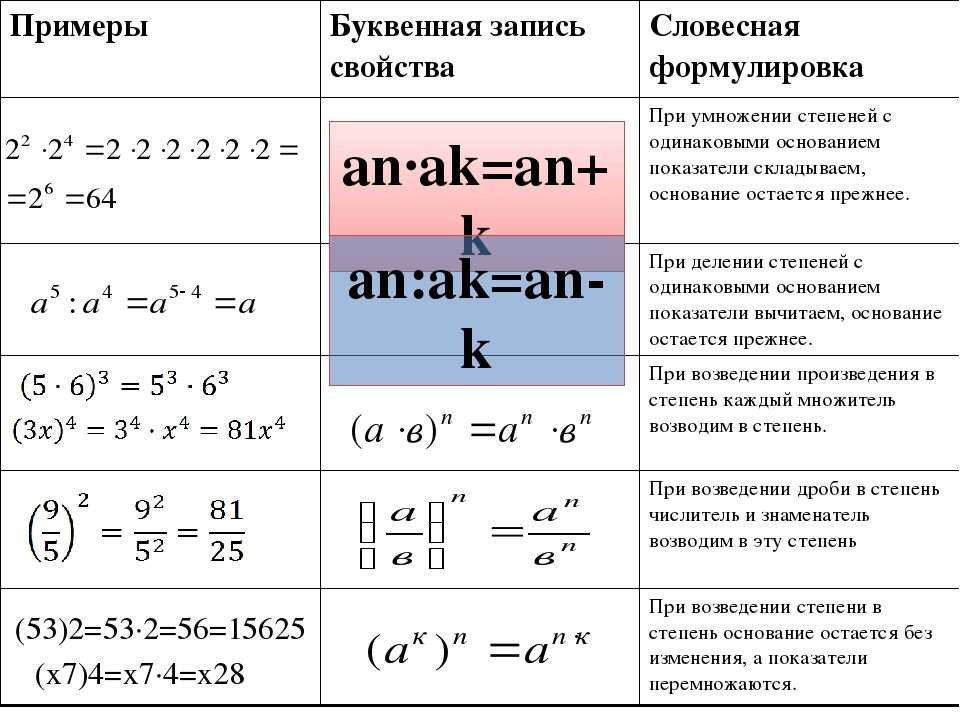
 Произведение степеней с одинаковыми показателями: \( {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\) Деление степеней с одинаковым основанием: \( …
Произведение степеней с одинаковыми показателями: \( {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\) Деление степеней с одинаковым основанием: \( …
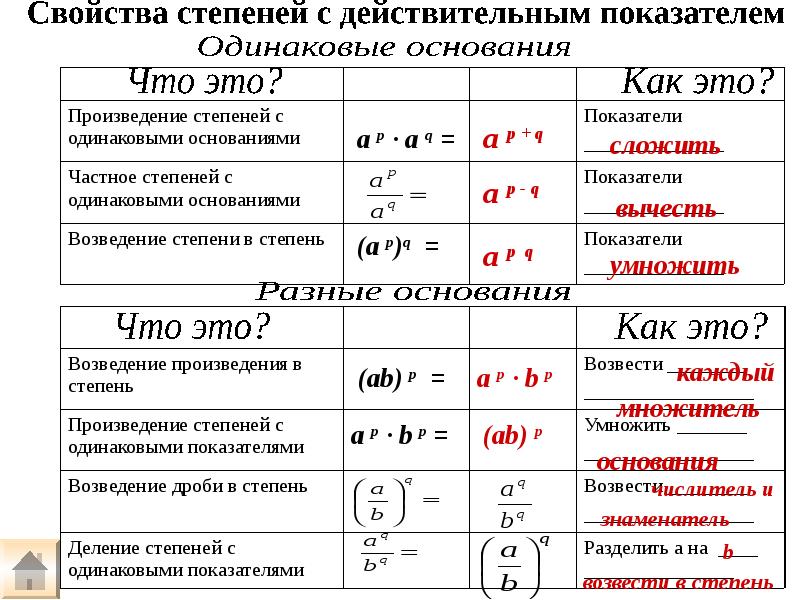 Сложение и вычитание степеней; Умножение степеней; Деление степеней; Примеры решения примеров с дробями, содержащими числа со степенями; Свойства степеней. …
Сложение и вычитание степеней; Умножение степеней; Деление степеней; Примеры решения примеров с дробями, содержащими числа со степенями; Свойства степеней. …
 Если степени обладают идентичными основаниями, то произведение таких степеней вычисляют путем сложения показателей и записи основания без изменений, то есть: …
Если степени обладают идентичными основаниями, то произведение таких степеней вычисляют путем сложения показателей и записи основания без изменений, то есть: …
 т.е. из двух степеней с одинаковым положительным показателем степени m/n меньше та, основание которой меньше, и больше та, основание которой больше. Если a и b – …
т.е. из двух степеней с одинаковым положительным показателем степени m/n меньше та, основание которой меньше, и больше та, основание которой больше. Если a и b – …
 Рассмотрено как умножать степени с одинаковым основанием, как делить степень на степень, если у них одинаковые основания. Приведены примеры с решениями
Рассмотрено как умножать степени с одинаковым основанием, как делить степень на степень, если у них одинаковые основания. Приведены примеры с решениями
Еще по теме: