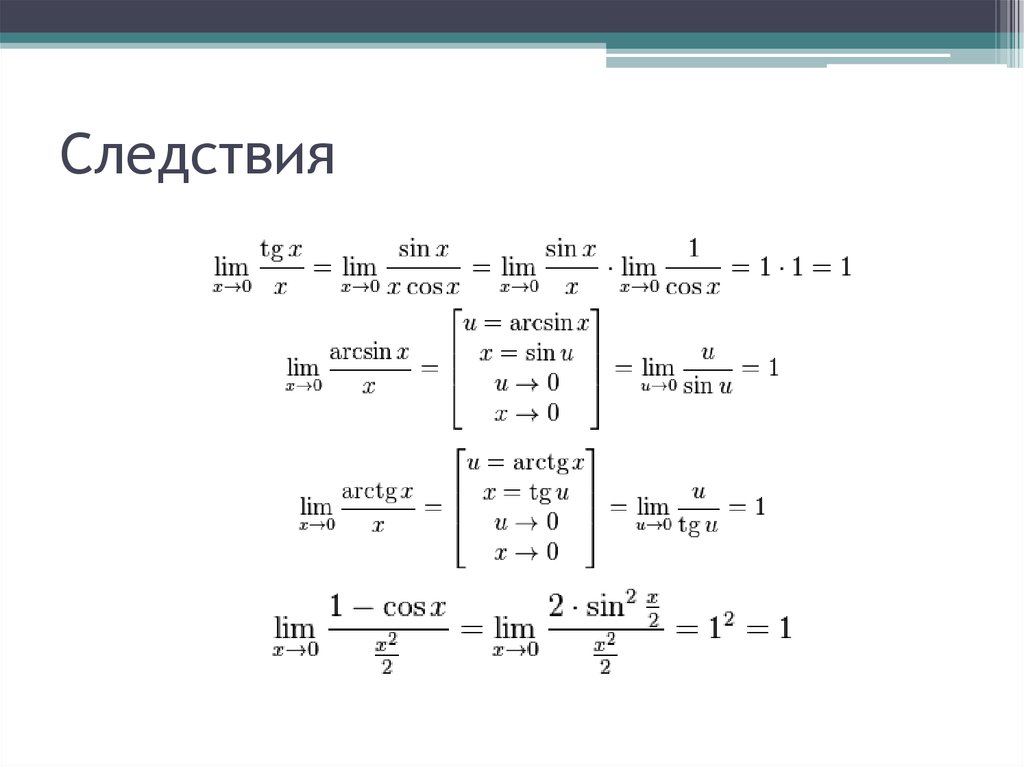
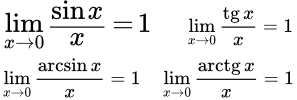Замечательных пределов существует несколько, но на практике у студентов-заочников в 95% случаев фигурируют два замечательных предела: Первый замечательный предел, …
Замечательных пределов существует несколько, но на практике у студентов-заочников в 95% случаев фигурируют два замечательных предела: Первый замечательный предел, …
 Примеры решений: 1 замечательный предел. Пример 1. Вычислить предел lim x → 0sin3x 8x. Решение. Первый шаг всегда одинаковый - подставляем предельное значение x = 0 …
Примеры решений: 1 замечательный предел. Пример 1. Вычислить предел lim x → 0sin3x 8x. Решение. Первый шаг всегда одинаковый - подставляем предельное значение x = 0 …

 Первый и второй замечательные⚠️ пределы: определение, как записываются. Примеры решений с 1 и 2 замечательным пределом☑️, доказательства
Первый и второй замечательные⚠️ пределы: определение, как записываются. Примеры решений с 1 и 2 замечательным пределом☑️, доказательства
 Для их раскрытия используют первый замечательный предел суть которого заключается в том, что предел отношения синус функции к аргументу, когда тот стремится к нулю …
Для их раскрытия используют первый замечательный предел суть которого заключается в том, что предел отношения синус функции к аргументу, когда тот стремится к нулю …
 Используя 1-й и 2-й замечательные пределы и их следствия, можно указать бесконечно малые функции при х→0, эквивалентные х: sinx, tgx, arcsinx, arctgx, ln(1+x), ex-1. При …
Используя 1-й и 2-й замечательные пределы и их следствия, можно указать бесконечно малые функции при х→0, эквивалентные х: sinx, tgx, arcsinx, arctgx, ln(1+x), ex-1. При …
 Первый замечательный предел, следствия, примеры. Определение первого замечательного предела:предел отношения синуса к аргументу, когда он стремится к …
Первый замечательный предел, следствия, примеры. Определение первого замечательного предела:предел отношения синуса к аргументу, когда он стремится к …
 В курсе высшей математики рассматриваются несколько пределов, получивших название «замечательные». Приведем некоторые из них: — первый замечательный предел; — …
В курсе высшей математики рассматриваются несколько пределов, получивших название «замечательные». Приведем некоторые из них: — первый замечательный предел; — …
 1. Первый замечательный предел: $\lim _ {x \rightarrow 0} \frac {\sin x} {x}=1$ Определение. Предел отношения синуса к его аргументу равен единице в случае, когда аргумент …
1. Первый замечательный предел: $\lim _ {x \rightarrow 0} \frac {\sin x} {x}=1$ Определение. Предел отношения синуса к его аргументу равен единице в случае, когда аргумент …
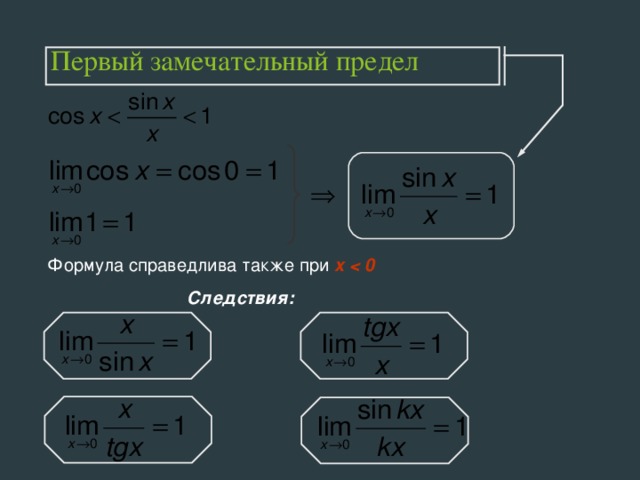
 Замечательные пределы и их следствия используются при раскрытии неопределённостей для нахождения других пределов функций. Первый замечательный предел при …
Замечательные пределы и их следствия используются при раскрытии неопределённостей для нахождения других пределов функций. Первый замечательный предел при …
 Замечательные пределы. п.1. Первый замечательный предел. Исследуем поведение функции f (x) = s i n x x вблизи x 0 = 0. Построим график. Заполним таблицу со значениями f (x) непосредственно вблизи x 0 = 0. В …
Замечательные пределы. п.1. Первый замечательный предел. Исследуем поведение функции f (x) = s i n x x вблизи x 0 = 0. Построим график. Заполним таблицу со значениями f (x) непосредственно вблизи x 0 = 0. В …
 Содержание: Замечательные пределы. Сравнение бесконечно малых функций. Первый замечательный предел. Число e и натуральные логарифмы. Второй замечательный …
Содержание: Замечательные пределы. Сравнение бесконечно малых функций. Первый замечательный предел. Число e и натуральные логарифмы. Второй замечательный …
 Для ее раскрытия следует заданную функцию свести под первый и второй замечательные пределы и их следствия. Для этого умножуєм и делим на выражения, которых не …
Для ее раскрытия следует заданную функцию свести под первый и второй замечательные пределы и их следствия. Для этого умножуєм и делим на выражения, которых не …
 В этом разделе вы найдете вычисления пределов с подробным решением: нахождение пределов с помощью разных подходов (зависит от типа неопределенности), через …
В этом разделе вы найдете вычисления пределов с подробным решением: нахождение пределов с помощью разных подходов (зависит от типа неопределенности), через …
Еще по теме:


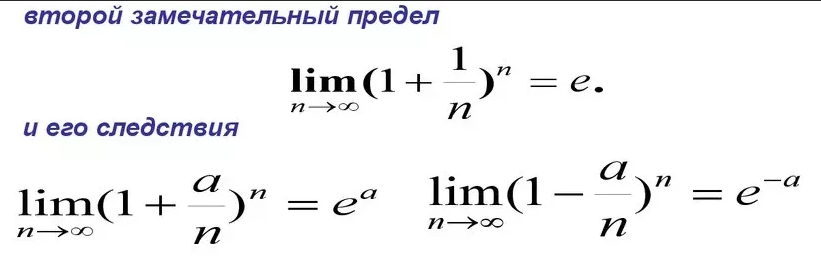












Еще по теме:







_images/1_matematicheskiy_analiz_(mn-va,f-ii,pred._i_neprer.f-ii)_74.jpg)