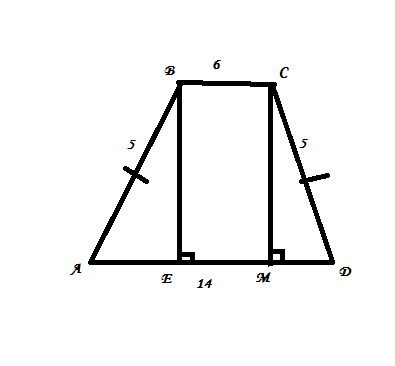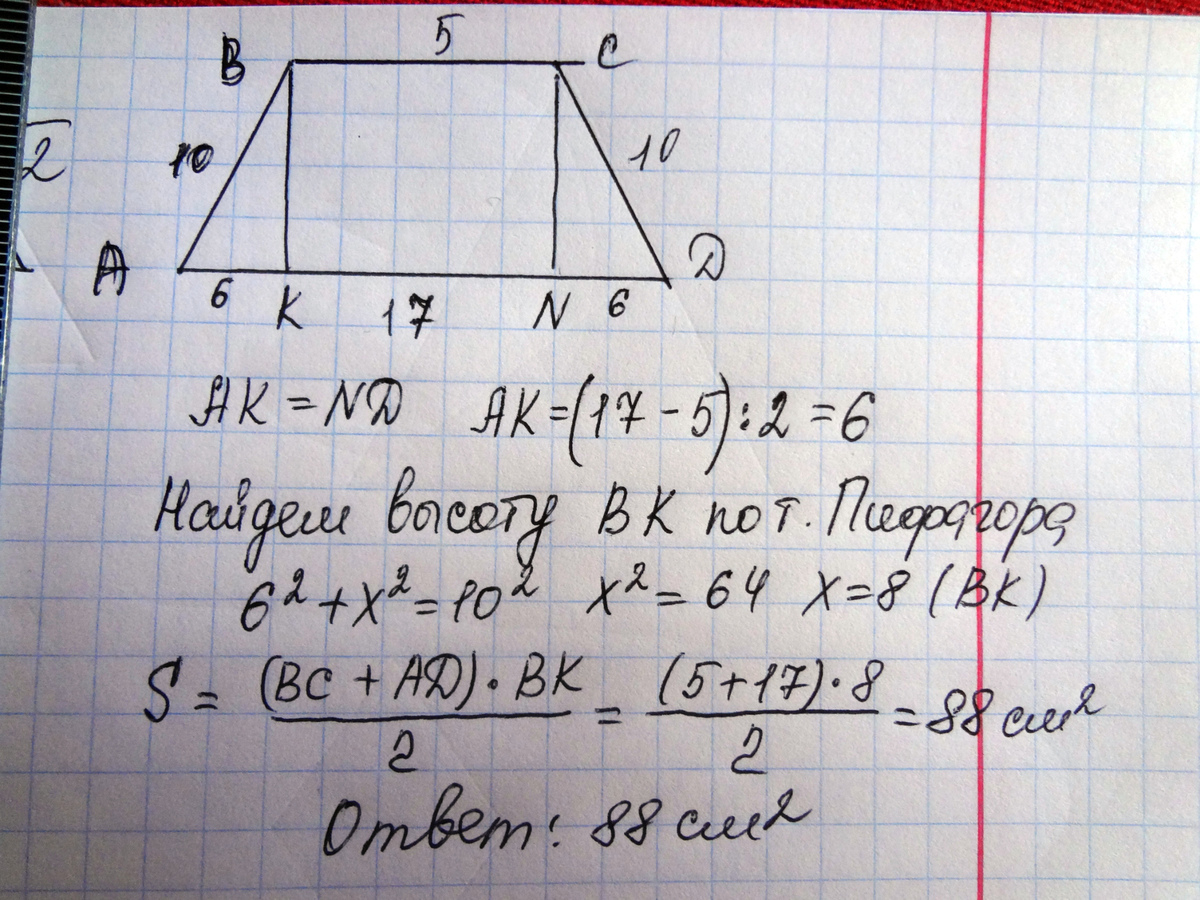 Sавсд = (ВС + АД) * ВН / 2 = (8 + 12) * 2 * tgα / 2 = 20 * tgα. Ответ: Периметр трапеции равен (4 / Sinα) + 20 см, площадь трапеции равна 20 * tgα.
Sавсд = (ВС + АД) * ВН / 2 = (8 + 12) * 2 * tgα / 2 = 20 * tgα. Ответ: Периметр трапеции равен (4 / Sinα) + 20 см, площадь трапеции равна 20 * tgα.
 ВН = √96 ≈ 9,8 см. Площадь трапеции равна: s = (12 + 8) / 2 · 9,8 = 20 / 2 · 9,8 = 10 · 9,8 = 98 см 2. Ответ: площадь трапеции равна 98 см 2.
ВН = √96 ≈ 9,8 см. Площадь трапеции равна: s = (12 + 8) / 2 · 9,8 = 20 / 2 · 9,8 = 10 · 9,8 = 98 см 2. Ответ: площадь трапеции равна 98 см 2.
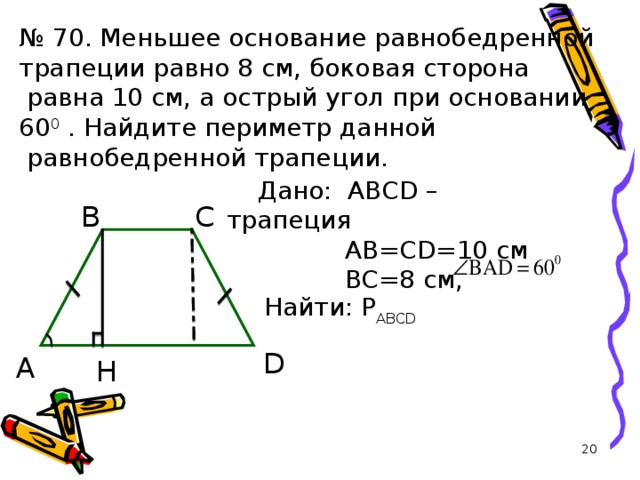
 Рассмотрим равнобедренную трапецию ABCD, с меньшим основание ВС=8 см, а большим AD=12 см. Острый угол 30°, а острый угол при большем основании, <A=<D=30°. Опустим …
Рассмотрим равнобедренную трапецию ABCD, с меньшим основание ВС=8 см, а большим AD=12 см. Острый угол 30°, а острый угол при большем основании, <A=<D=30°. Опустим …
 Определение. Равнобедренная трапеция — это трапеция у котрой боковые стороны равны. На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной …
Определение. Равнобедренная трапеция — это трапеция у котрой боковые стороны равны. На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной …
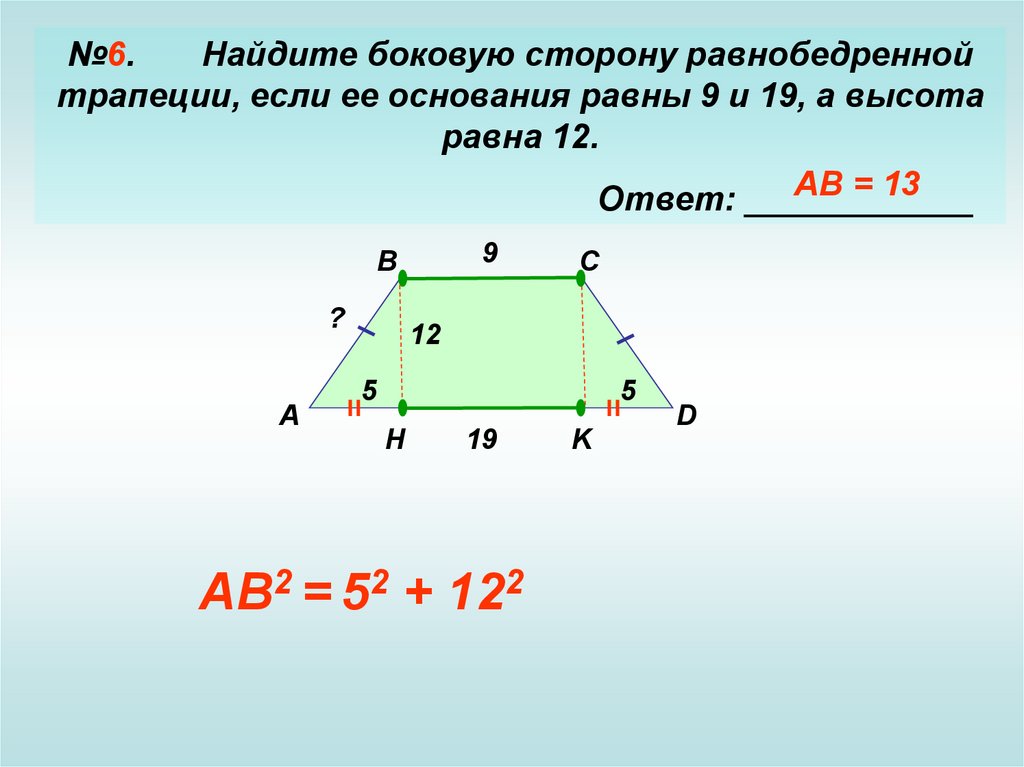
 Дана равнобедренная трапеция. Ее основания равны 8 см и 12 см, а высота равна 5 см. Найдите площадь трапеции. Решение: a = 8 см; b = 12 см; h = 5 см; Подставляем в формулу: S = (8 + 12) * 5 / 2 = 10 * 5 = 50 …
Дана равнобедренная трапеция. Ее основания равны 8 см и 12 см, а высота равна 5 см. Найдите площадь трапеции. Решение: a = 8 см; b = 12 см; h = 5 см; Подставляем в формулу: S = (8 + 12) * 5 / 2 = 10 * 5 = 50 …
 где: a - боковая сторона трапеции. d1, d2 - диагонали трапеции. b - основание трапеции. Данная формула основана на теореме Пифагора, применяемой к треугольникам, образованным диагоналями и …
где: a - боковая сторона трапеции. d1, d2 - диагонали трапеции. b - основание трапеции. Данная формула основана на теореме Пифагора, применяемой к треугольникам, образованным диагоналями и …
 Дано: в трапеции abcd основания ab и cd равны 8 см и 12 см соответственно, а высота трапеции равна 6 см. Найдите площадь трапеции.
Дано: в трапеции abcd основания ab и cd равны 8 см и 12 см соответственно, а высота трапеции равна 6 см. Найдите площадь трапеции.
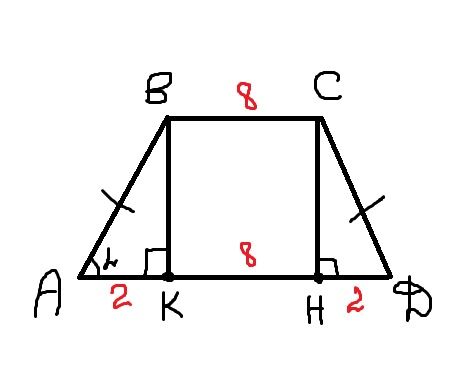
 Без применения косинусов и синусов эта задача не решается. Для этого вас и тренируют, чтоб учили основы арифметики. Сторона трапеции равна 4, периметр равен 8+12+4+4=28
Без применения косинусов и синусов эта задача не решается. Для этого вас и тренируют, чтоб учили основы арифметики. Сторона трапеции равна 4, периметр равен 8+12+4+4=28
 Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции.
Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции.
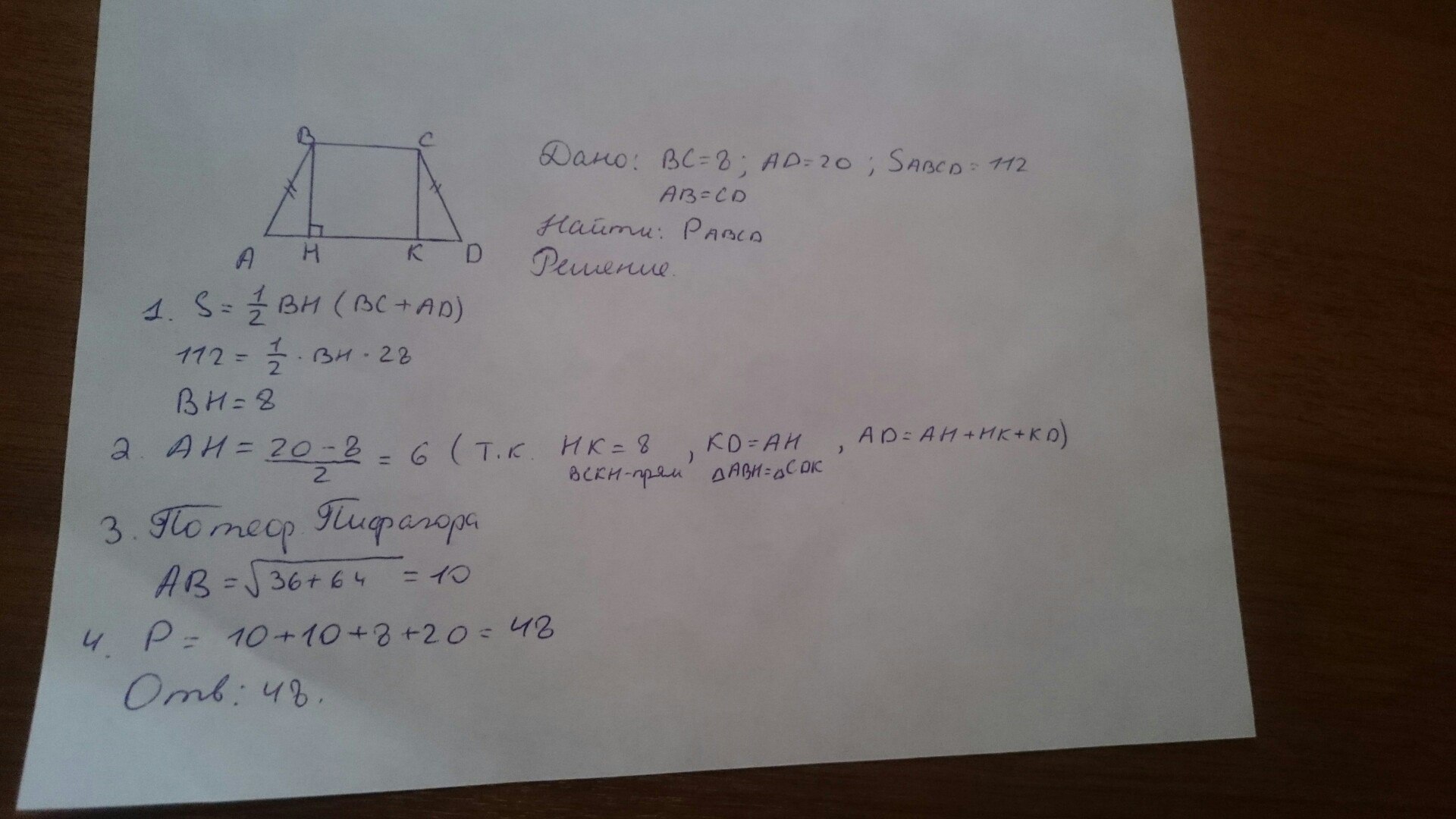
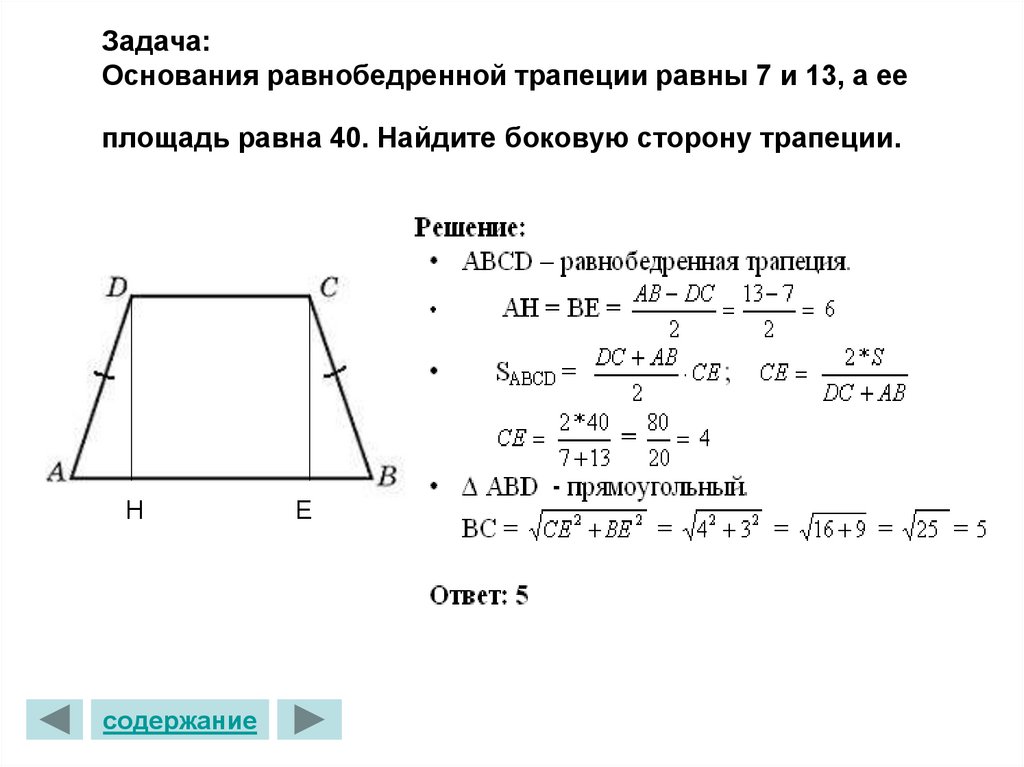
 Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.
Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.
 В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот …
В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот …
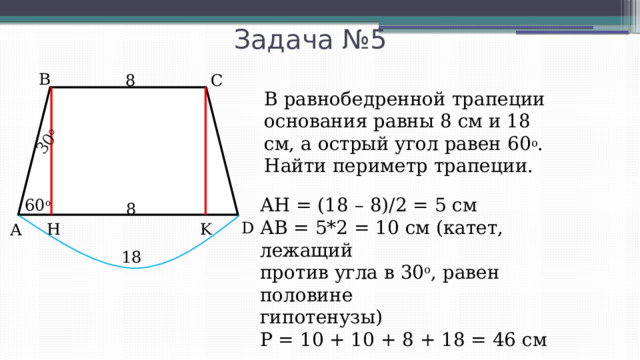
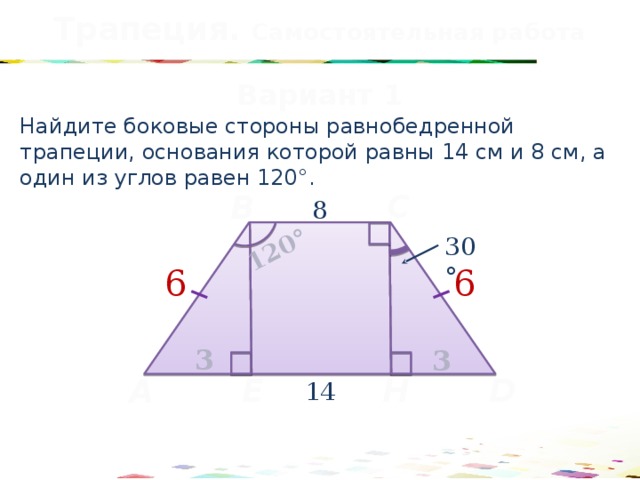
 В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции. Решение. Площадь …
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции. Решение. Площадь …
 Формула периметра равнобедренной трапеции: Периметр = a + b + 2c. где: a и b – основания трапеции; c – боковая сторона; 2. Пошаговый алгоритм вычисления …
Формула периметра равнобедренной трапеции: Периметр = a + b + 2c. где: a и b – основания трапеции; c – боковая сторона; 2. Пошаговый алгоритм вычисления …
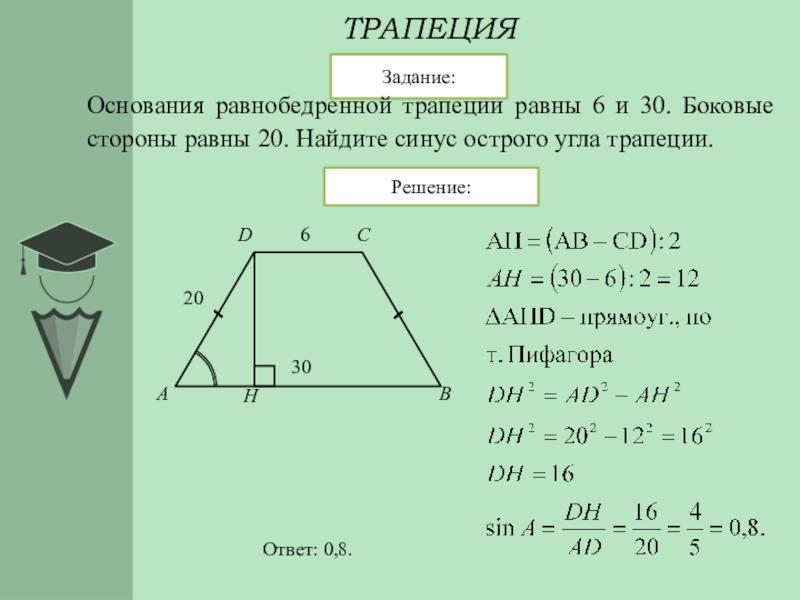
 Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
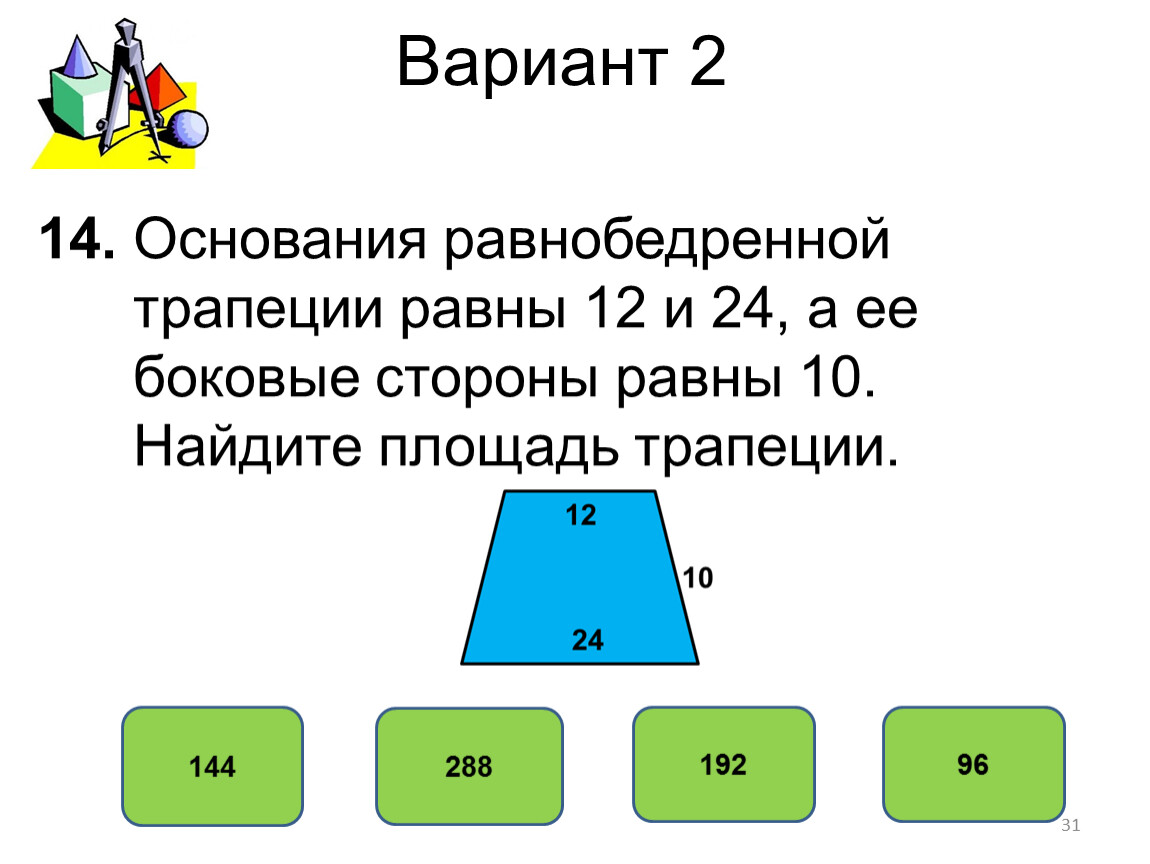
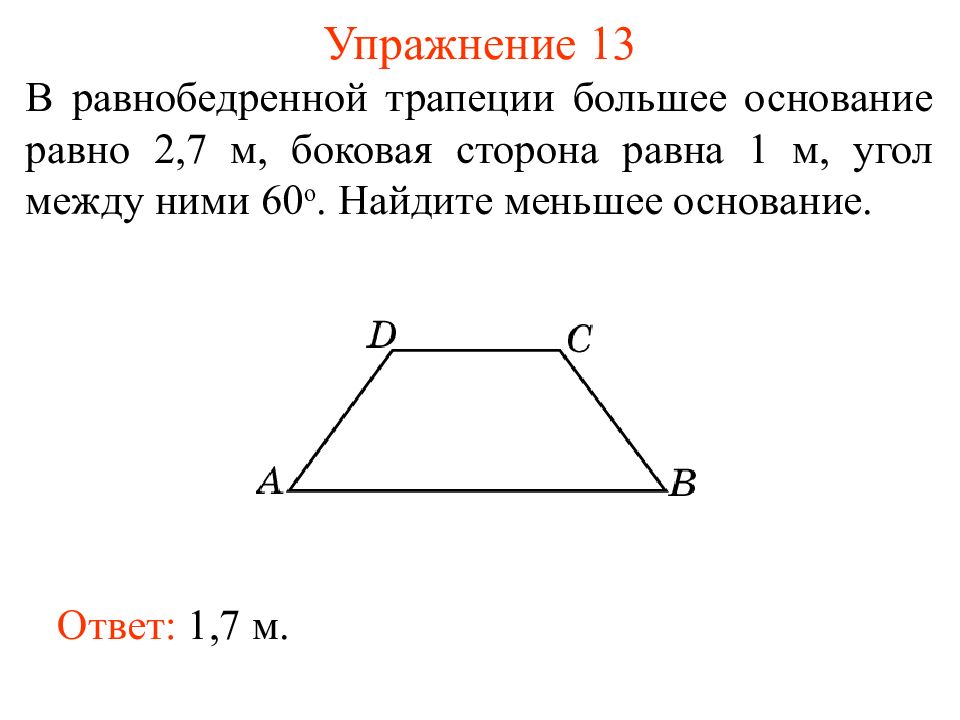 Найдите площадь равнобедренной трапеции, если его основания равны 8см'. '.mb_convert_case('и', MB_CASE_TITLE, 'UTF-8') 12см. , а боковая сторона-10см …
Найдите площадь равнобедренной трапеции, если его основания равны 8см'. '.mb_convert_case('и', MB_CASE_TITLE, 'UTF-8') 12см. , а боковая сторона-10см …
Еще по теме:








Еще по теме: