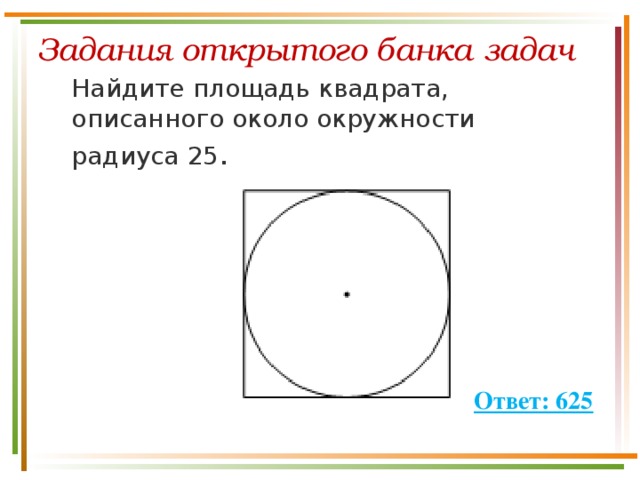
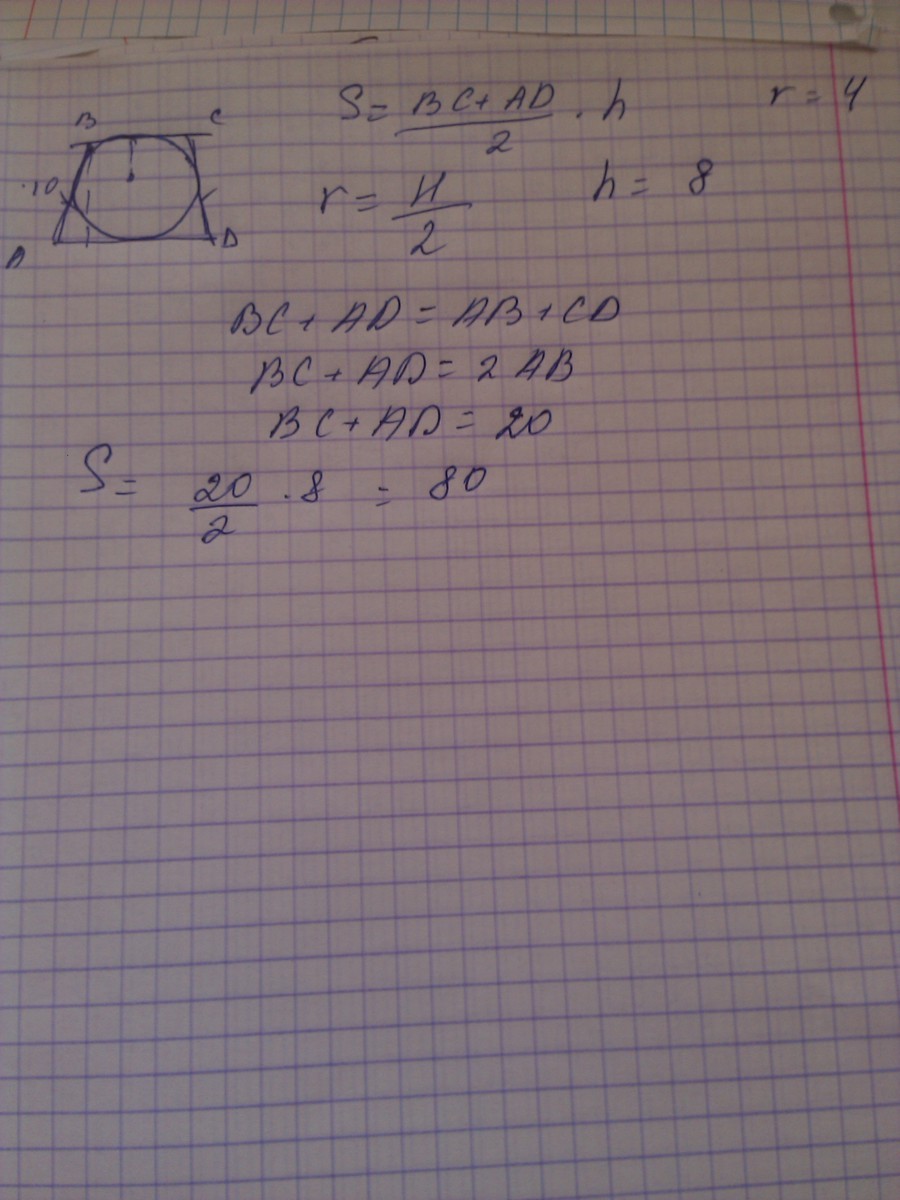Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани равна 10 см. …
Площадь квадрата можно найти через радиус вписанной окружности по формуле: S = 4 * r^2, где S - площадь квадрата, r - радиус окружности, вокруг которой описан квадрат. …
Площадь квадрата: 13832.2623. Итак, площадь квадрата, описанного вокруг окружности радиуса 83, составляет примерно 13832.2623 квадратных единиц. Эта задача …
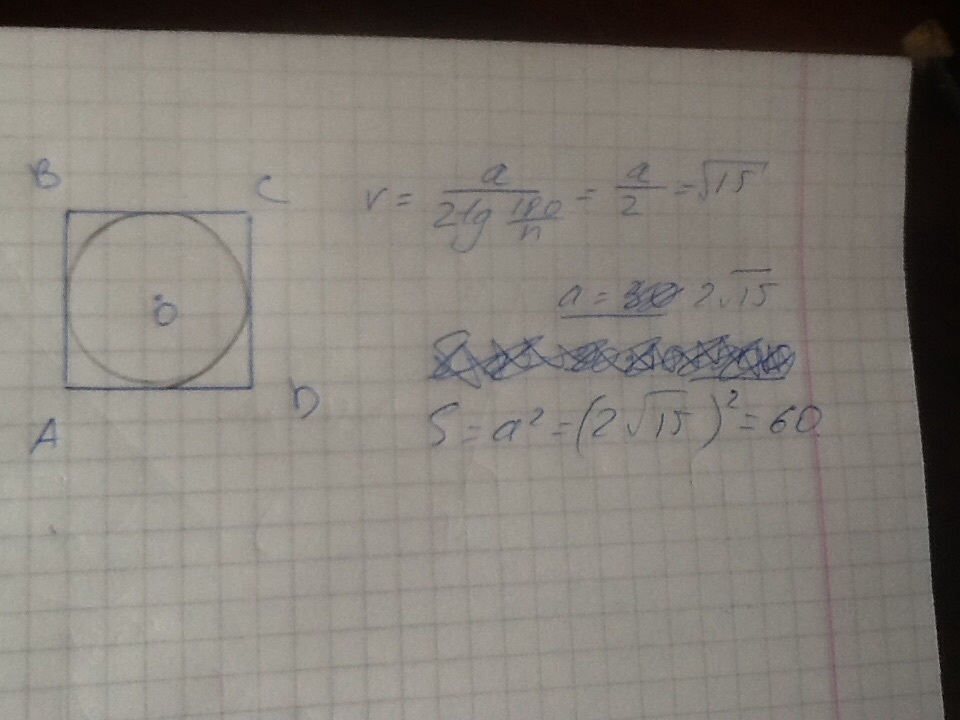
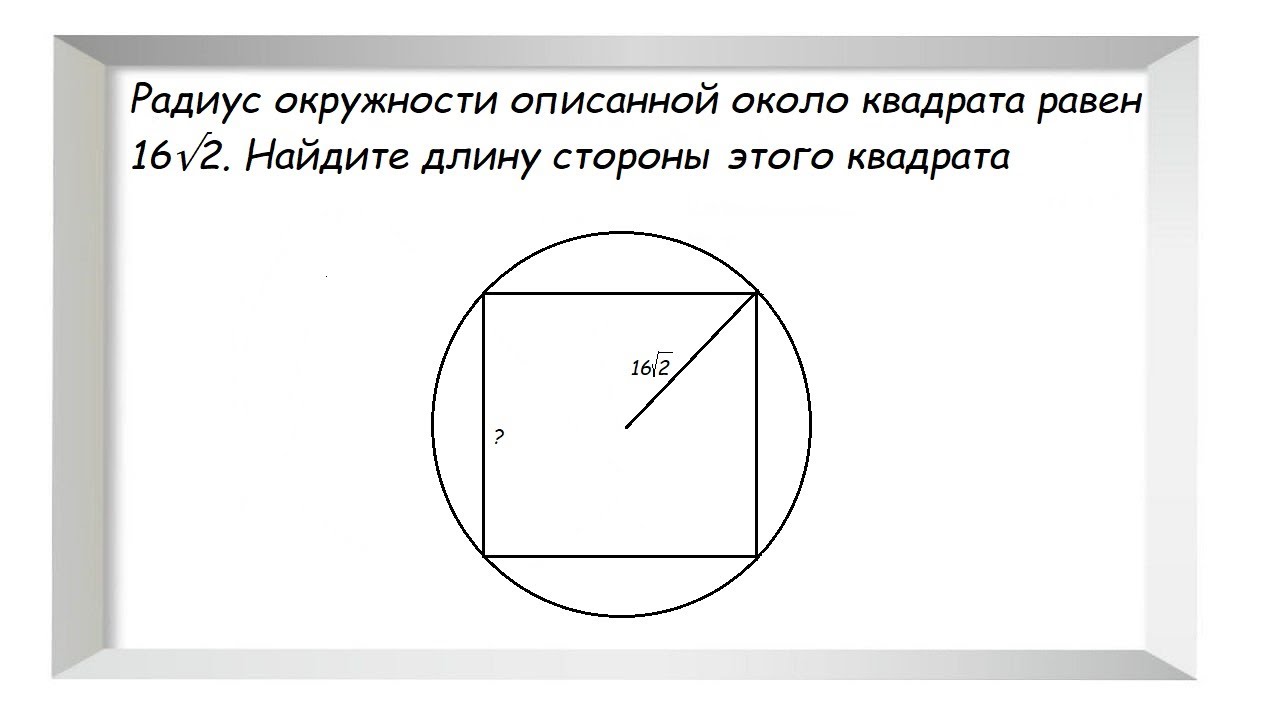
Найдите площадь квадрата, описанного вокруг окружности радиуса 83. Решение . Пусть R и D соответственно радиус и диаметр окружности, a — сторона квадрата.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83. Решение задачи: Стороны квадрата являются касательными к окружности, следовательно, отрезок, …
Для начала, найдем диагональ квадрата, описанного вокруг окружности радиуса 83. Диагональ квадрата составляет два радиуса окружности, то есть 83 + 83 = 166.
Площадь квадрата по радиусу 83 описанной окружности равна 13778
Данный онлайн калькулятор поможет найти площадь квадрата, описанного вокруг окружности, зная радиус окружности, диаметр окружности, длину окружности, площадь …
Так как радиус 83, то поперечник равняется 166. С этого следует, что сторона квадрата также равняется 166, а площадь квадрата считаем по формуле S = a^2.
Используем формулу для площади квадрата, описанного вокруг окружности: Площадь квадрата = (Диаметр окружности)^2 Радиус окружности равен 83, следовательно, диаметр окружности равен 2 * 83 = 166.
Формула. S = 4⋅S к π. Пример. К примеру, посчитаем площадь описанного квадрата. Площадь окружности, вокруг которой описан этот квадрат, равна Sк = 5 см²: S = 4⋅5 ÷ 3.14 ≈ 6.37 см².
Найдите площадь квадрата, описанного вокруг окружности радиуса 83. Решение . Пусть R и D соответственно радиус и диаметр окружности, a — сторона квадрата.
Подставим в формулу известное нам значение радиуса вписанной окружности и найдем площадь квадрата: s = 4 * (83^2) = 4 * 6889 = 27556 (условных единиц квадратных). …
Так как радиус 83, то диаметр равняется 166. С этого следует, что сторона квадрата также равняется 166, а площадь квадрата считаем по формуле S = a^2.
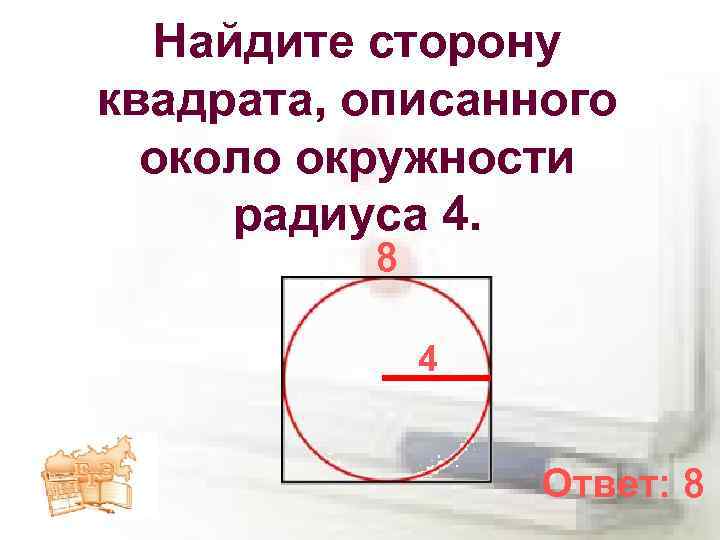
Найдите площадь квадрата, описанного около окружности радиуса 32. Решение: Пусть R и D соответственно радиус и диаметр окружности, a — сторона …
Еще по теме:
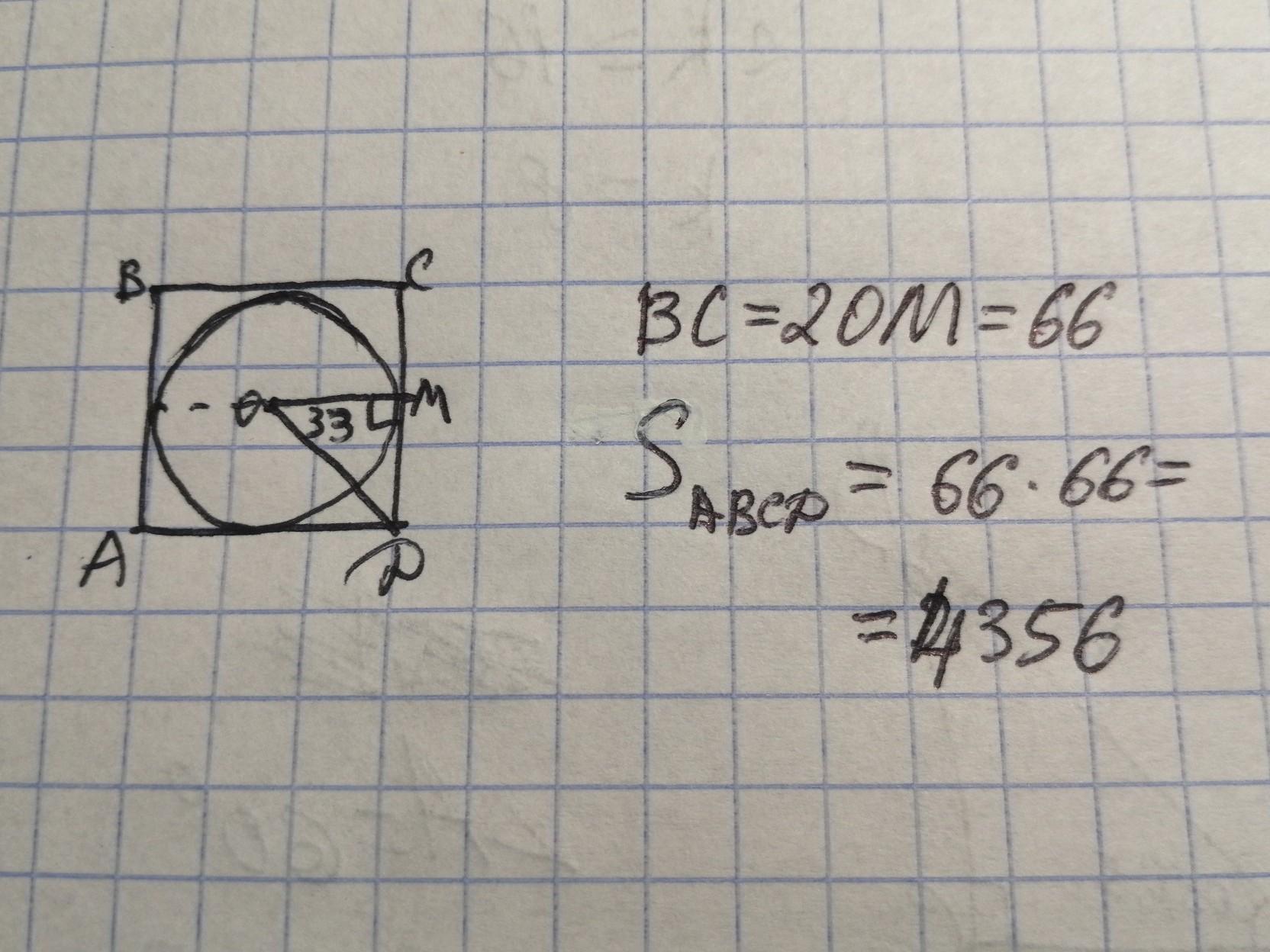
Еще по теме:
.jpg)
