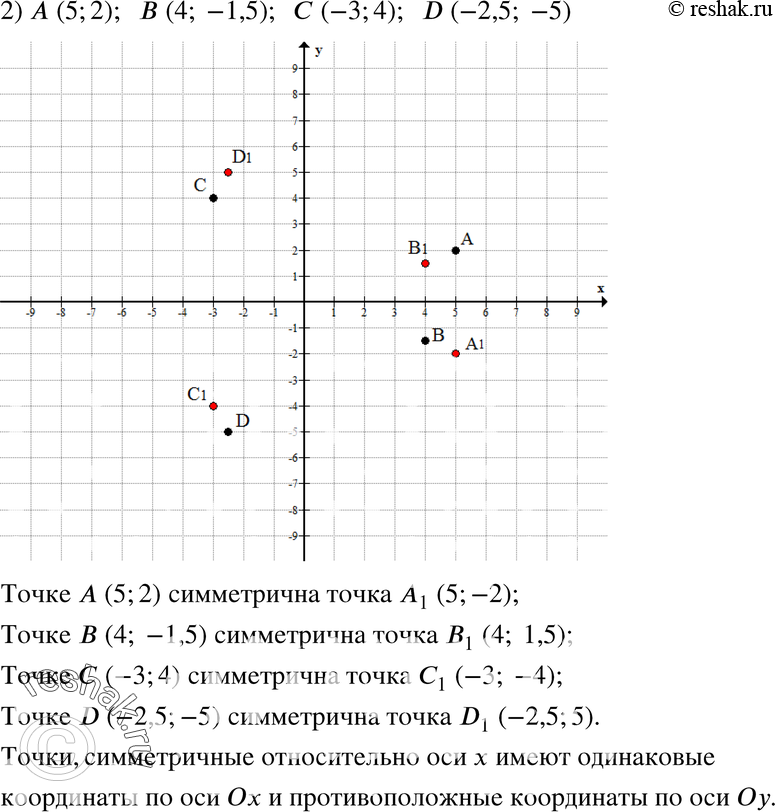
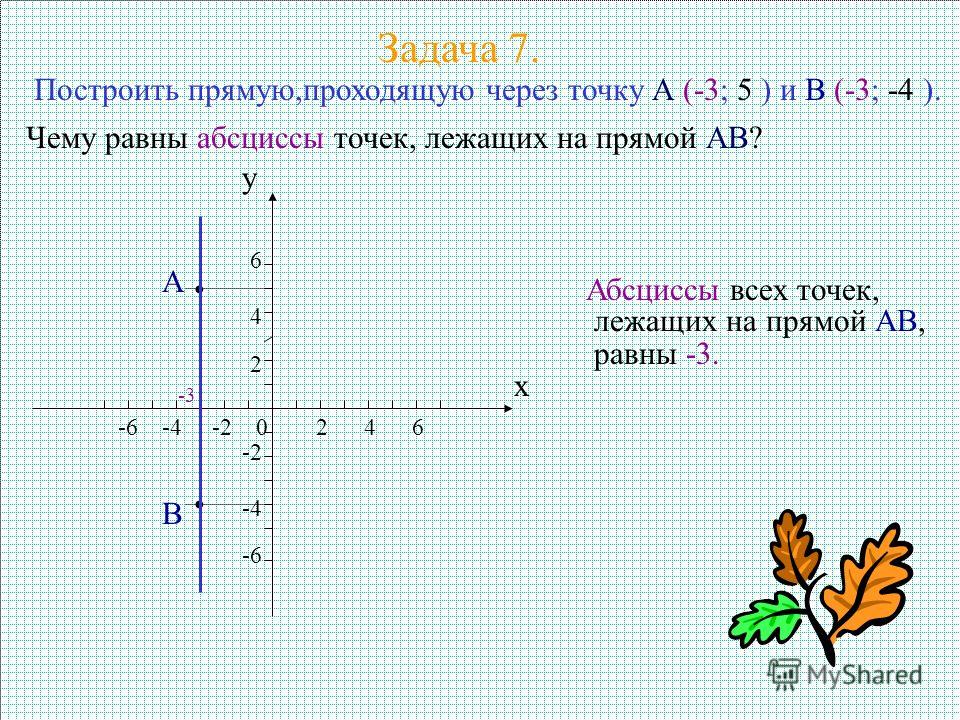
N-равноудалена от точек Р и К, значит |PN|=|KN| N лежит на оси абсцисс, значит N(x;0) Координаты вектора PN={x+1;-3} Координаты вектора KN={x;-2} Длина вектора …
После возведения левой и правой частей в квадрат и упрощений получим: (x + 1)2 + (y - 3)2 = x2 + (y + 2)2 x2 + 2x + 1 + y2 - 6y + 9 = x2 + y2 + 4y + 4 или 2x - 10y + 6 = 0 При у = 0 …
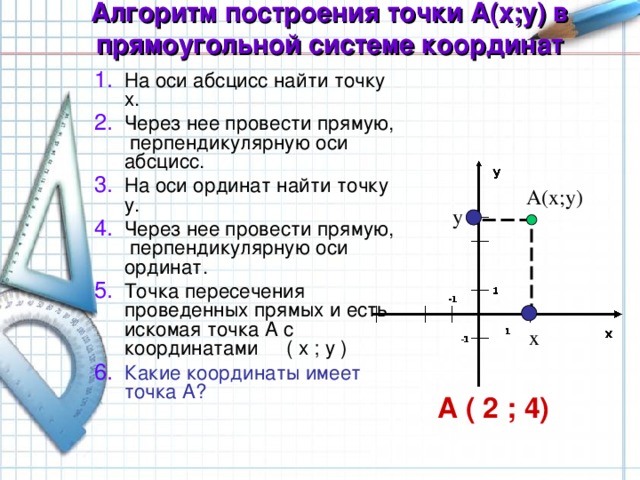
Нахождение абсциссы точки на числовой оси. Если точка задана на числовой оси, то ее абсцисса равна соответствующему числу. Например, если точка a имеет координату 3 на числовой оси, то.
Координаты середины (x,y) отрезка с конечными точками (x₁,y₁) и (x₂,y₂) могут быть найдены следующим образом: x = (x1 + x2) / 2 y = (y1 + y2) / 2 Для отрезка PK с …
Для того чтобы найти координаты точки n, которая лежит на оси абсцисс и равноудалена от точек p(-1;3) и k(0;2), мы можем воспользоваться формулой для нахождения середины …
Задача заключается в том, чтобы найти координаты точки n, которая лежит на оси абсцисс и равноудалена от двух заданных точек p(-1;3) и k(0;2).Перед тем, как …
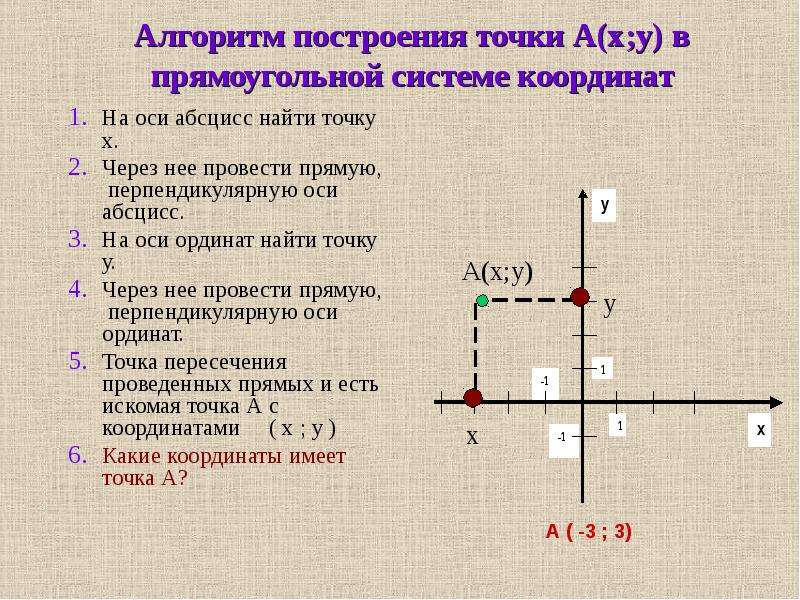
* Найдите координаты точки n, лежащей на оси абсцисс и равноудаленной от точек Р(–1; 3) и k(0; 2). ОТВЕТ: n(–3; 0).
4.Найдите координаты точки n,лежащей на оси абсцисс и равноудаленной от точек p(2;4) и k(5;-1). Ответ от Оксана Вернуться к списку вопросов
Ось абсцисс - это ось Х, и координата всех точек у на этой оси равна 0 Итого - нам надо найти точку вида (x;0) р(2 4) и к(5 -1) равноудалённую от р(2;4) и к(5;-1) √((2-x)²+(4-0)²) = …
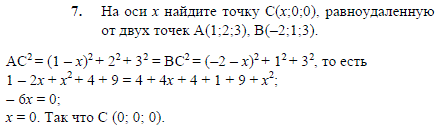обозначим координату точки n - x построим на осях точки Р и К , равноудалённость n, можно определить как равенство гипотенуз треугольников образованных проекциями …
Найдите координаты точки, принадлежащей оси ординат и равноудалённой от точек d(-2; -3) и Е(4; ГДЗ 4 класс
Пусть точка n(х; 0) равноудалена от точек p(2;4) и К (5;-1). Тогда NР=NК корень (х-2)^2+4^2=корень (х-2)^+1
* Найдите координаты точки n, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( - 1; 3 ) и К( 0; 2 ). 2 вариант.
Это точка N(х; 0). Поэтому (x+1)^2+9=x^2+4. Сам решишь?
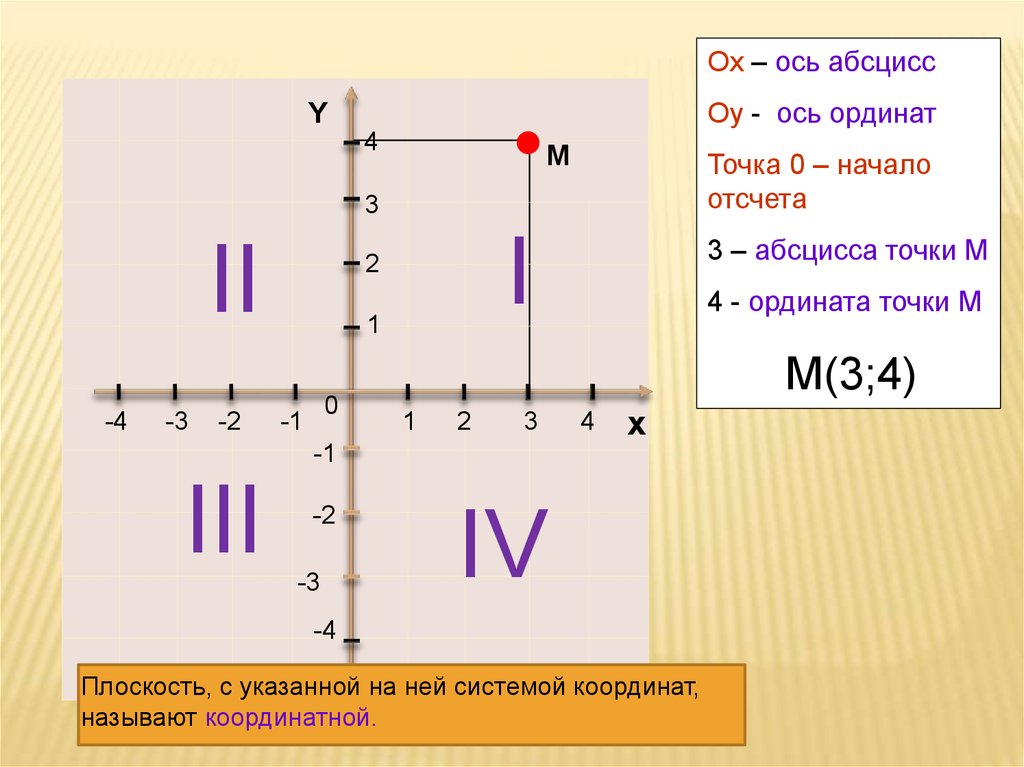4.Найдите координаты точки n,лежащей на оси абсцисс и равноудаленной от точек p (-1;3) и k (0;2). 5*. В равнобедренном треугольнике основание равно 16 см, а …
Еще по теме:
Еще по теме:
