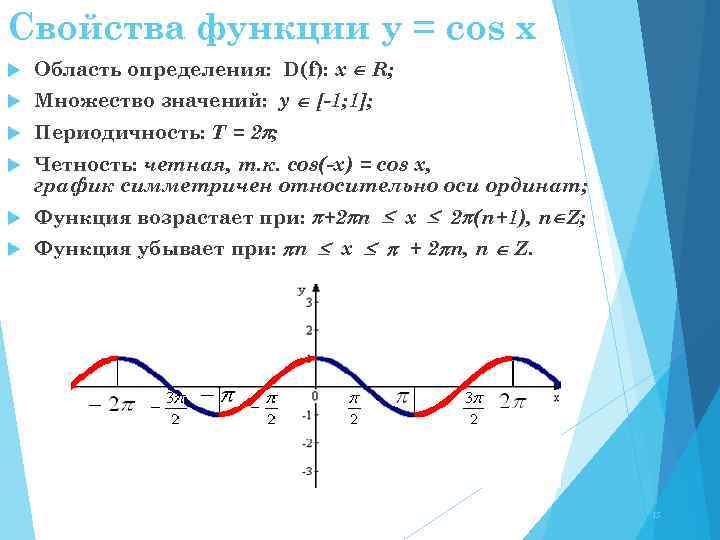
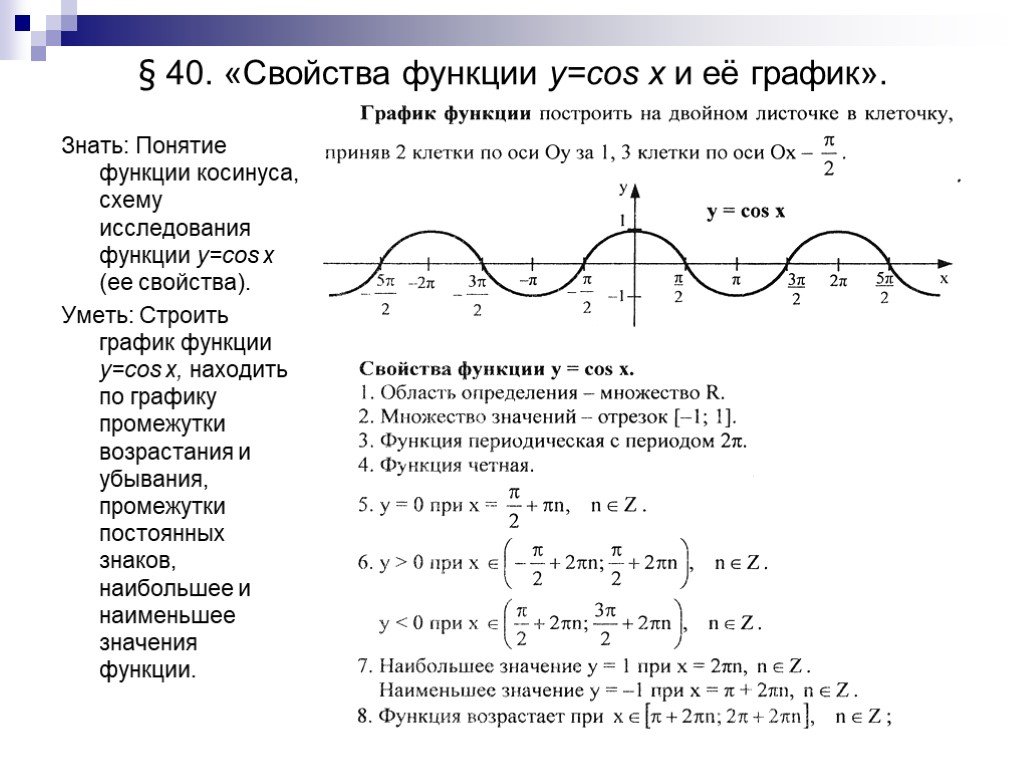
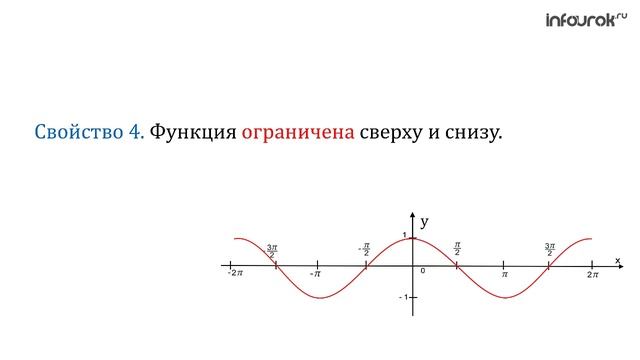
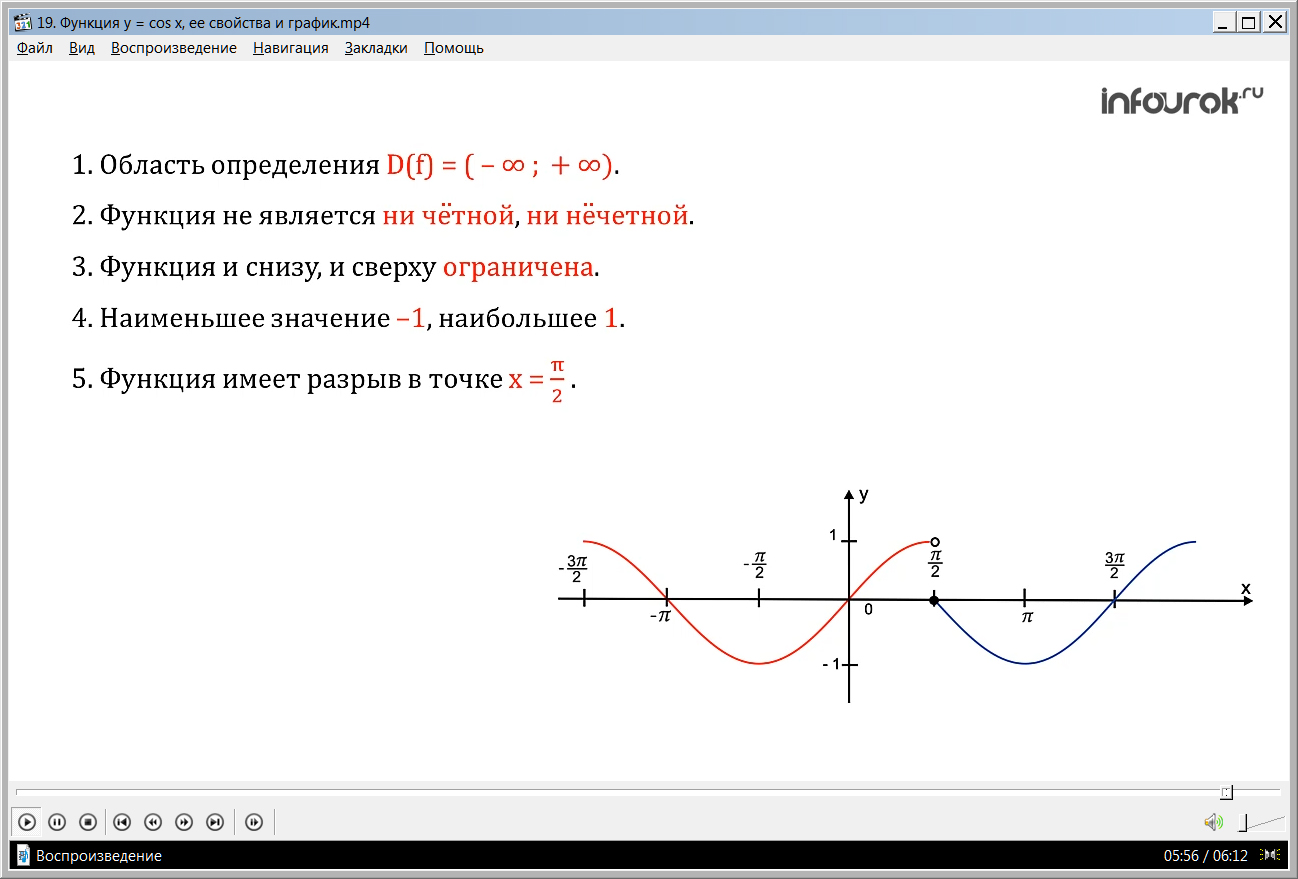
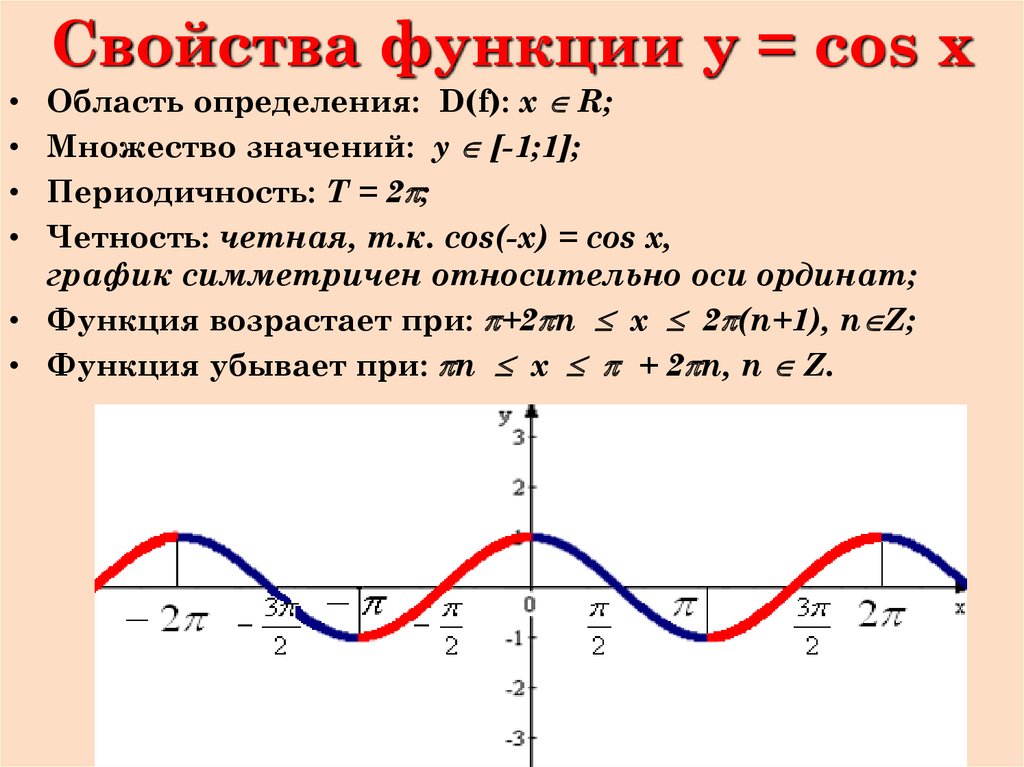
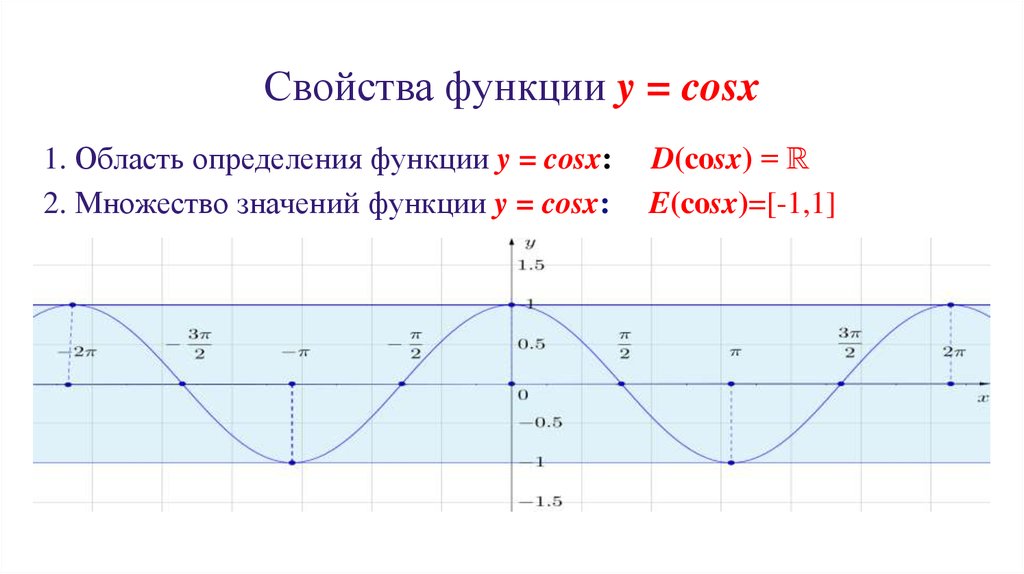
 Свойства функции y =cos x . 1. Область определения \ (x\in\mathbb {R}\) - множество действительных чисел. 2. Функция ограничена сверху и снизу $$ -1\leq cosx\leq 1 $$ …
Свойства функции y =cos x . 1. Область определения \ (x\in\mathbb {R}\) - множество действительных чисел. 2. Функция ограничена сверху и снизу $$ -1\leq cosx\leq 1 $$ …
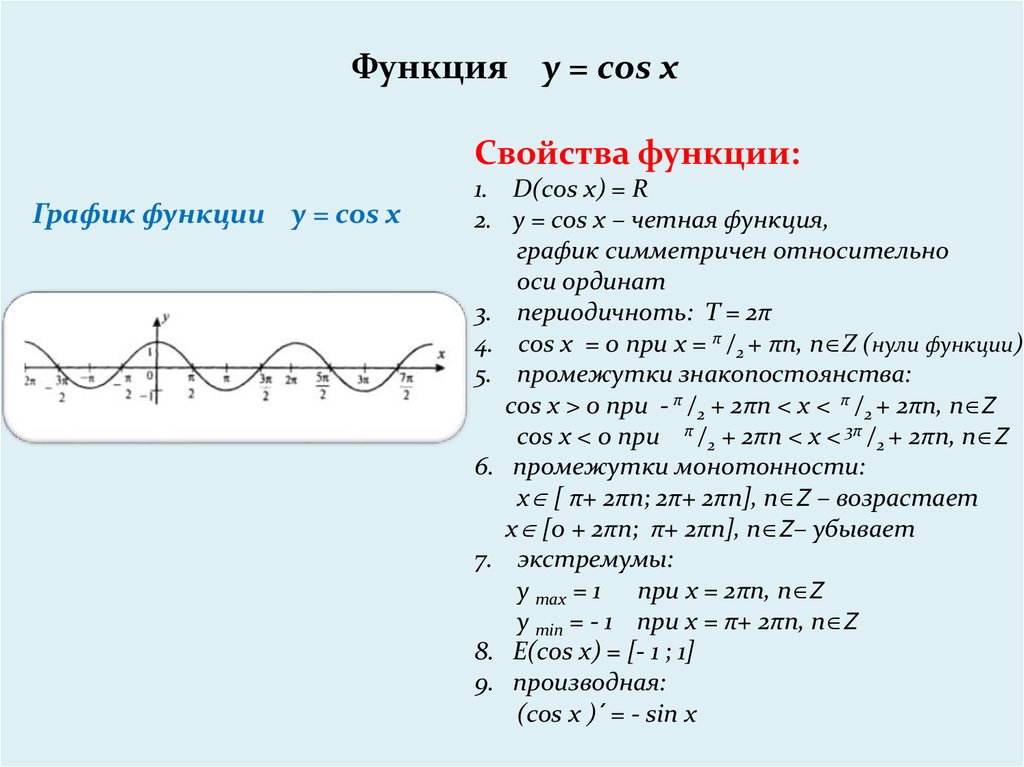
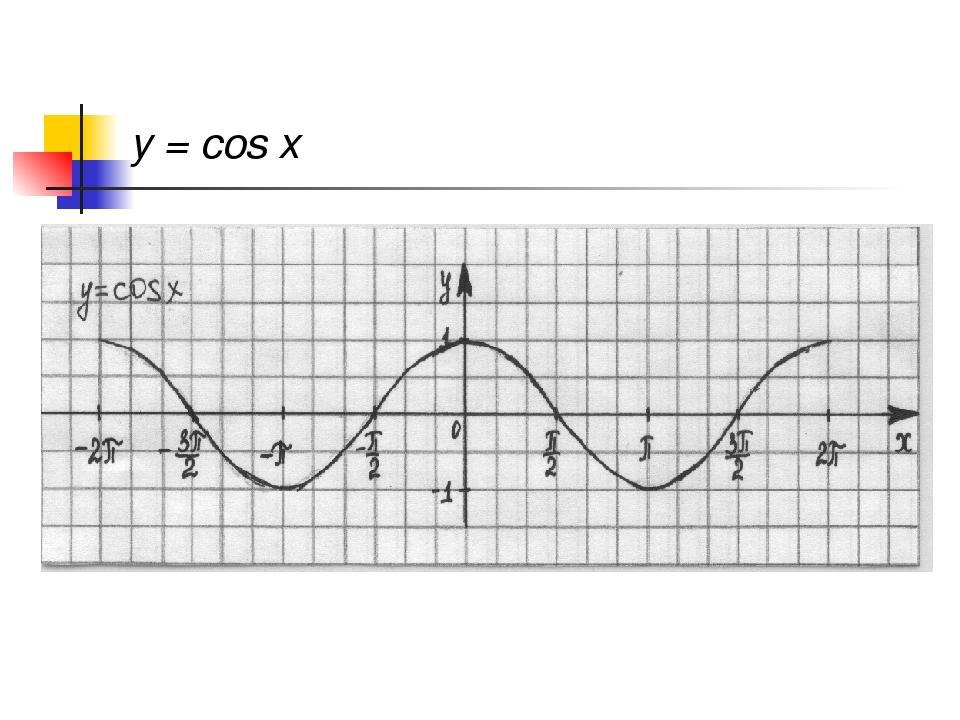 Перечислим свойства тригонометрической функции.
Перечислим свойства тригонометрической функции.
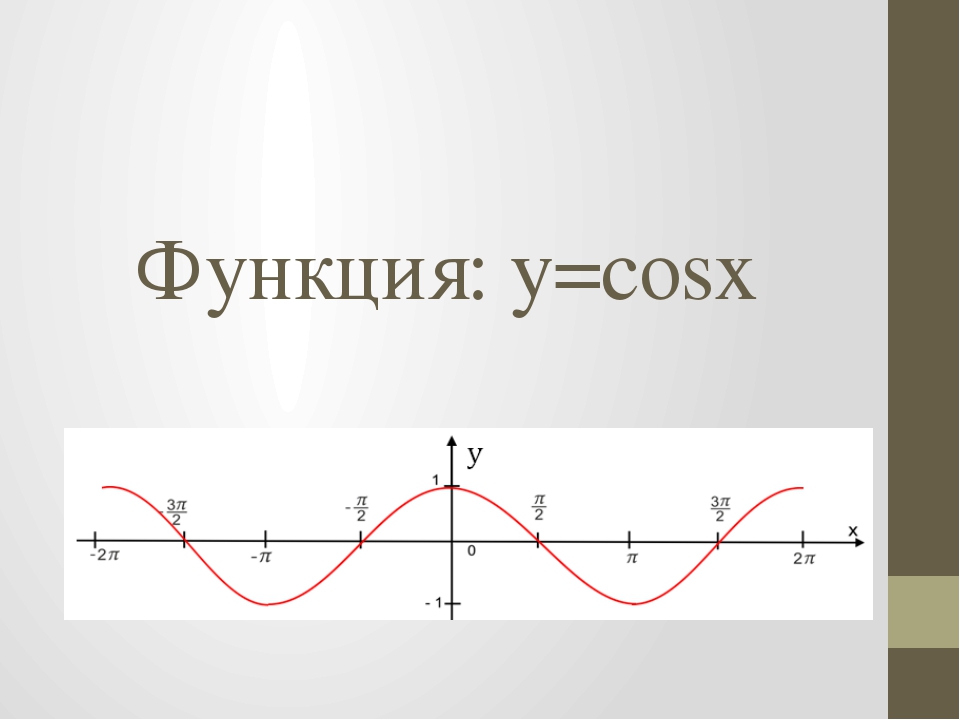
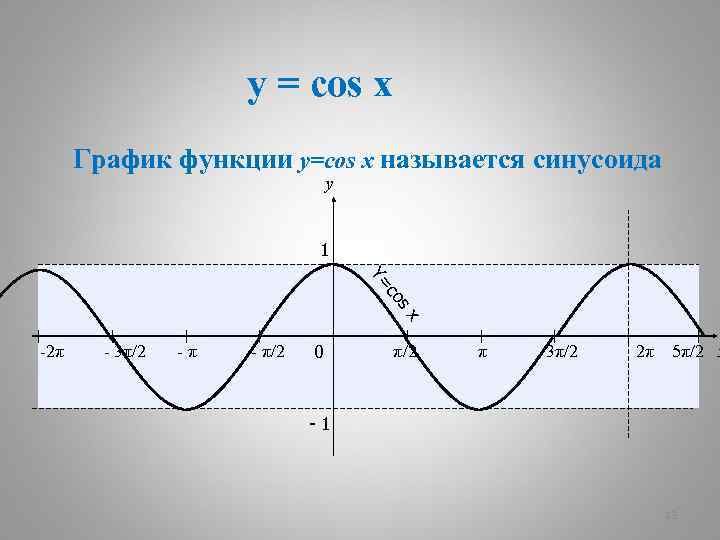
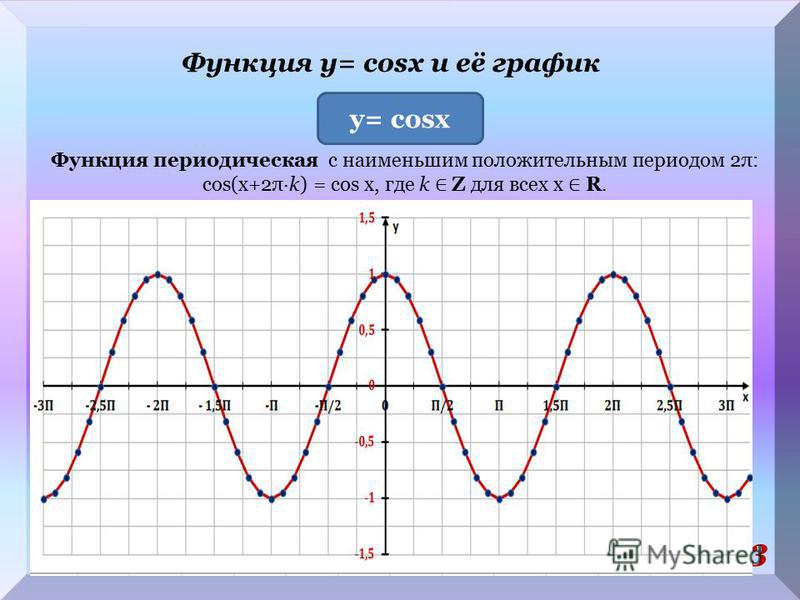
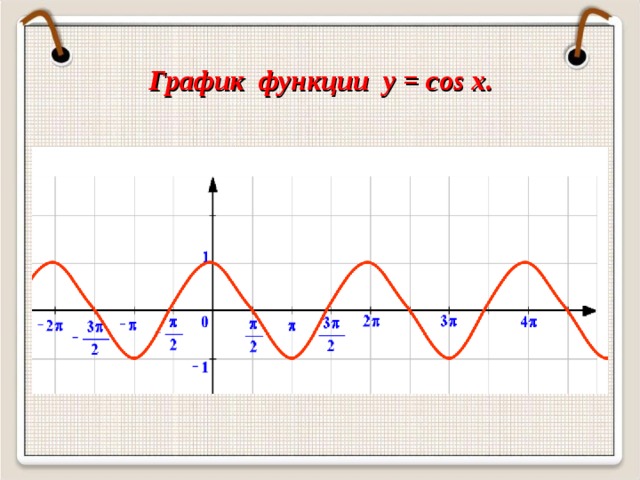
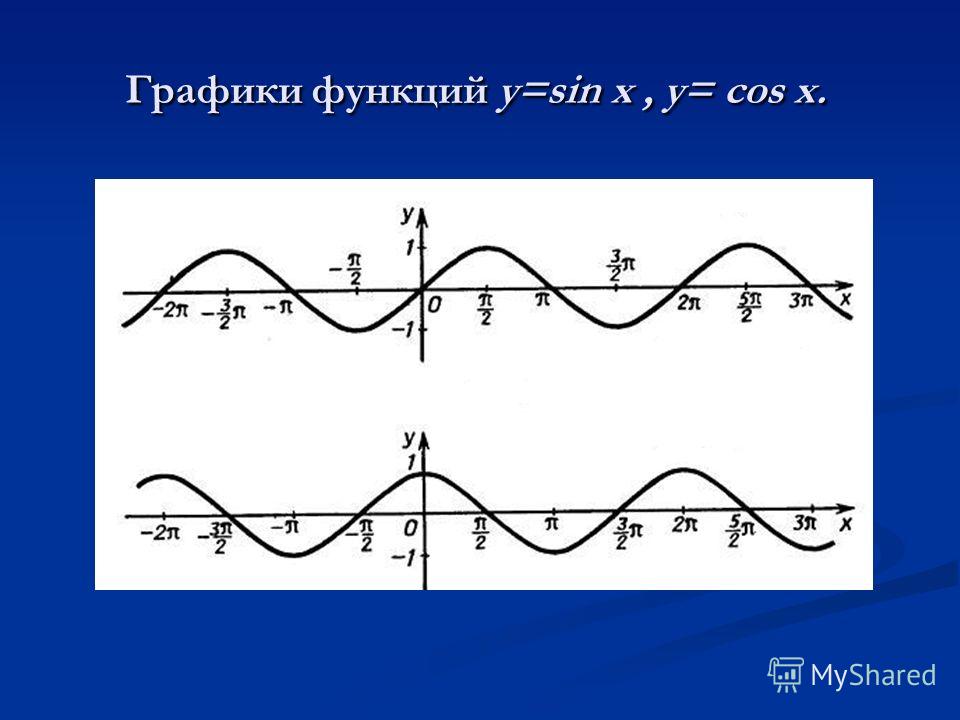
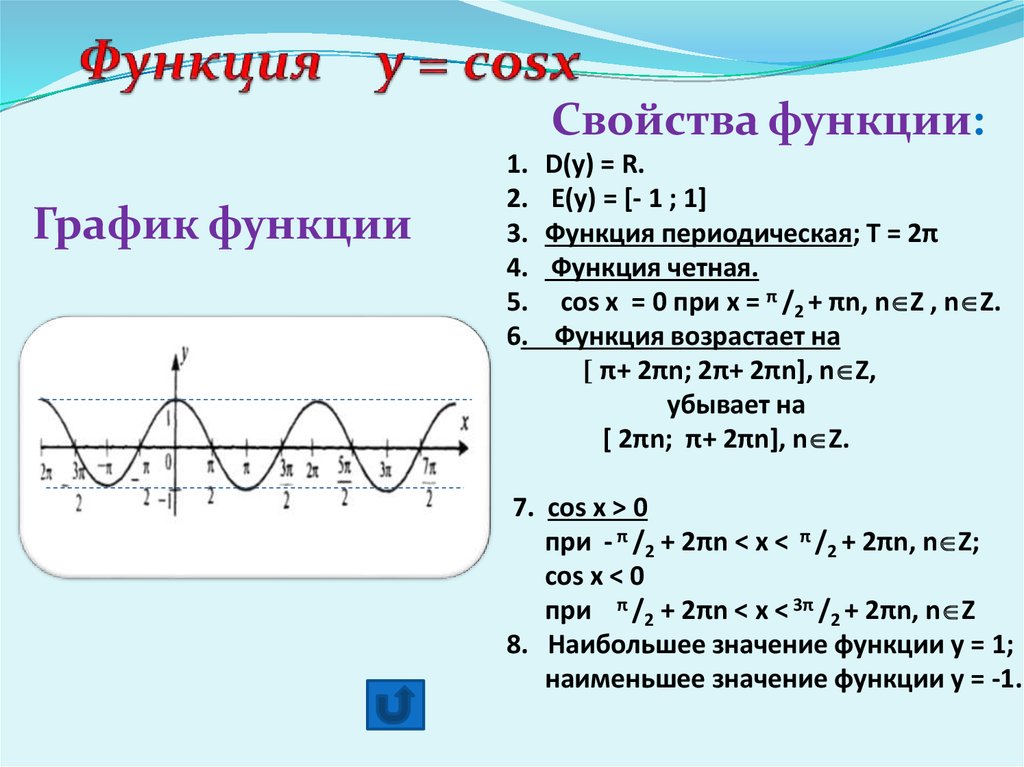 Функция y cosx определяется как косинус числового аргумента x. Ее графиком является косинусоида - волнообразная кривая, колеблющаяся между 1 и -1. Рассмотрим подробнее ее свойства. …
Функция y cosx определяется как косинус числового аргумента x. Ее графиком является косинусоида - волнообразная кривая, колеблющаяся между 1 и -1. Рассмотрим подробнее ее свойства. …
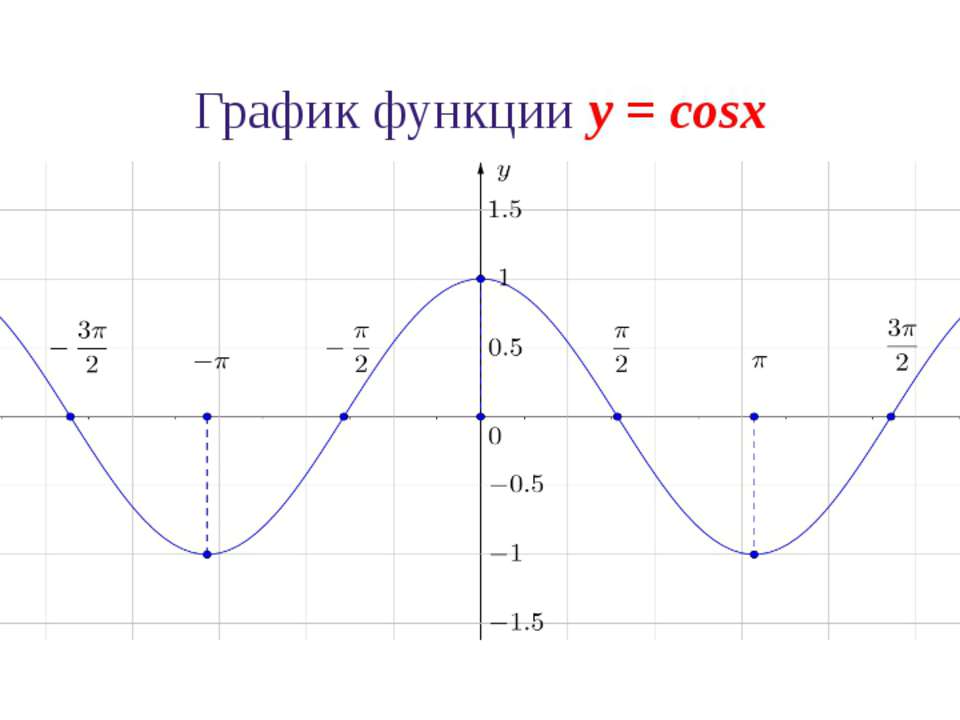
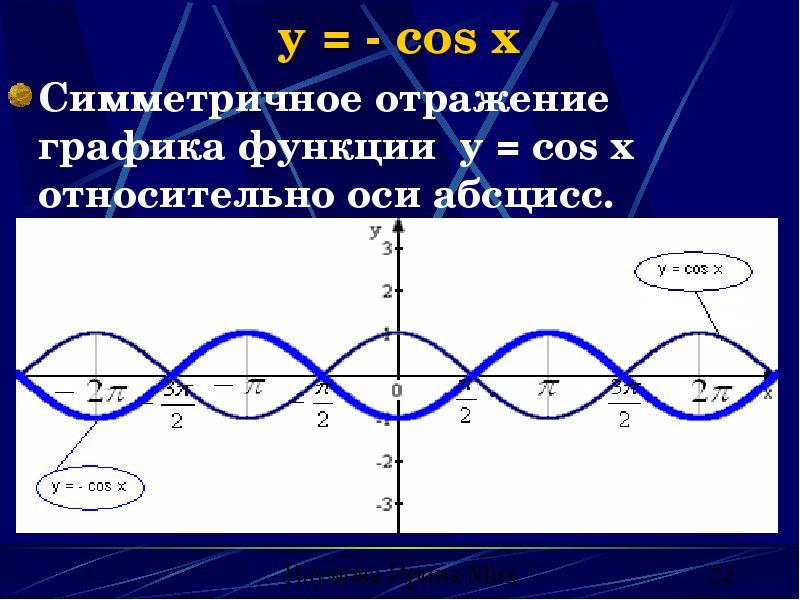
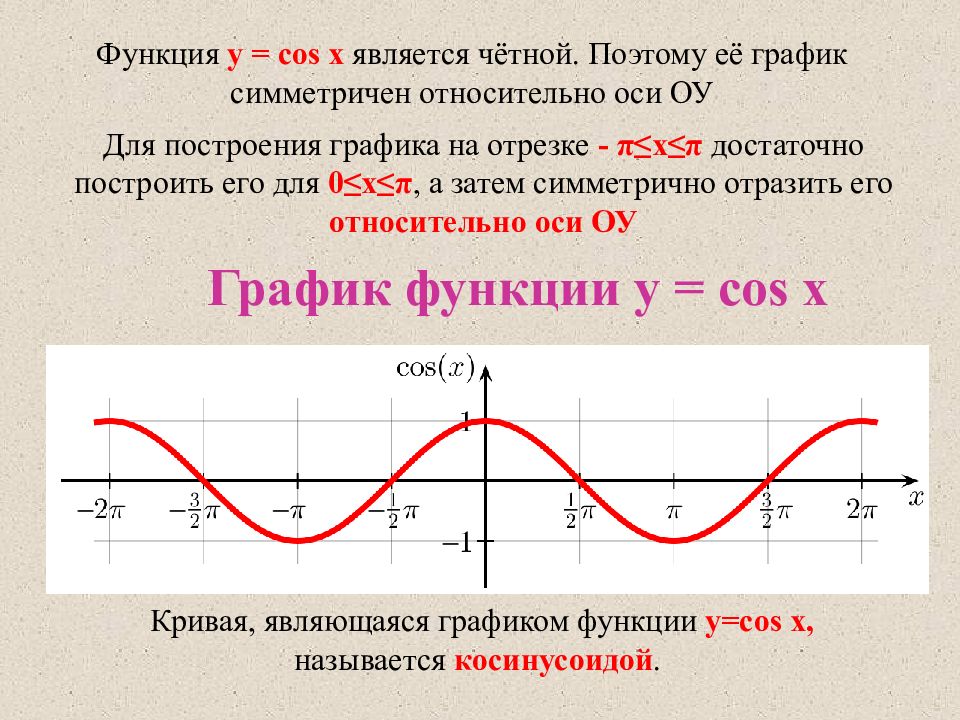
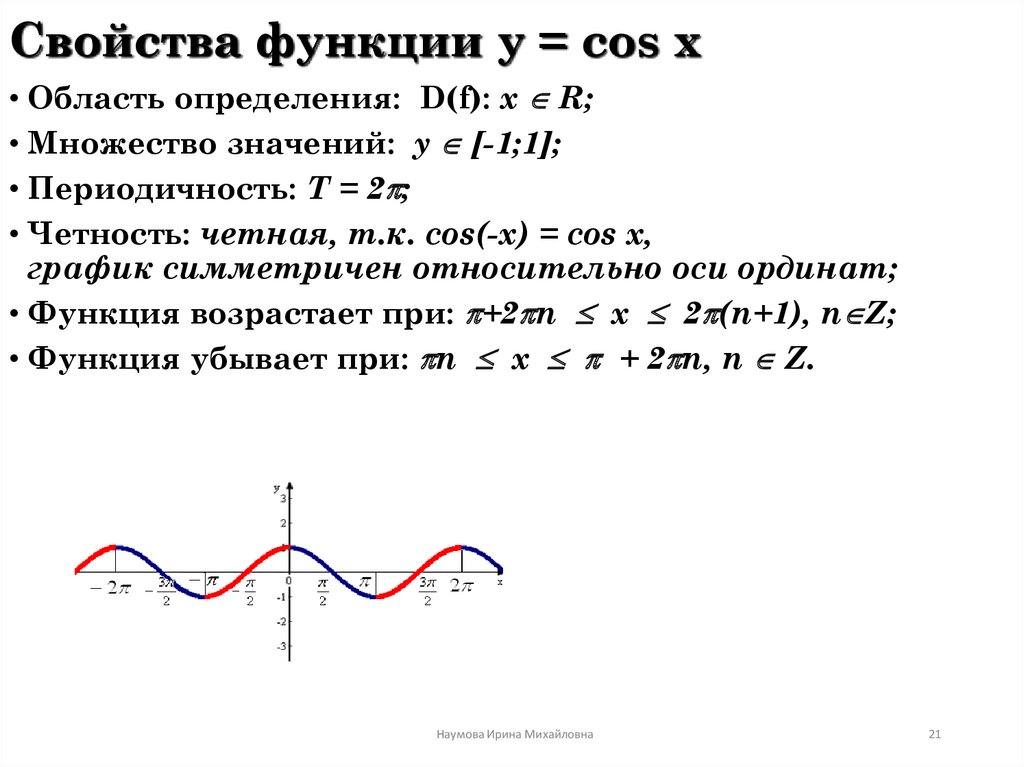
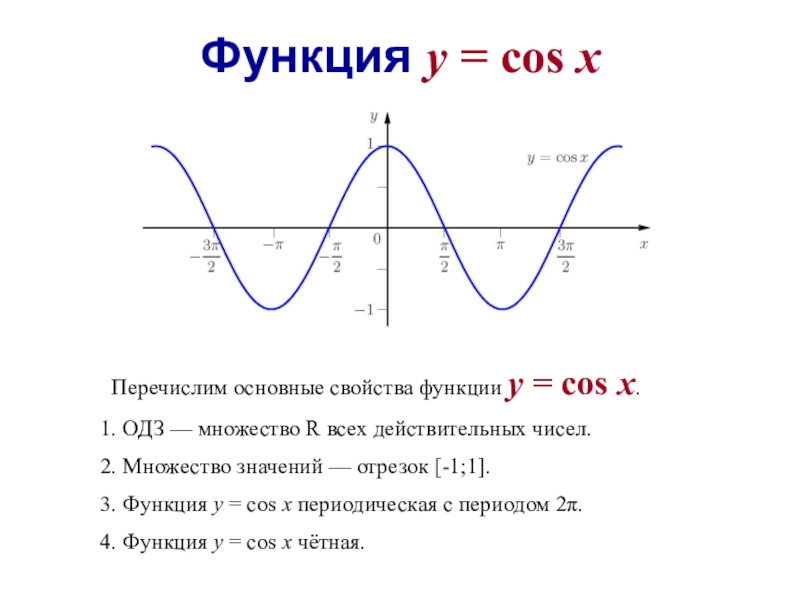
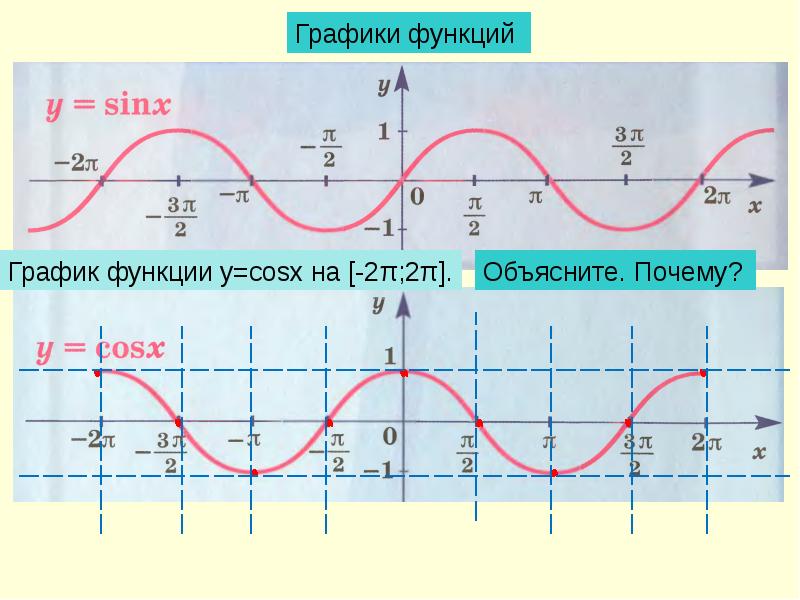 Функция y = cosx является четной (cos(-х) = cosх, для всех х ∈ R, и график косинуса симметричен относительно оси ординат (OY)).
Функция y = cosx является четной (cos(-х) = cosх, для всех х ∈ R, и график косинуса симметричен относительно оси ординат (OY)).
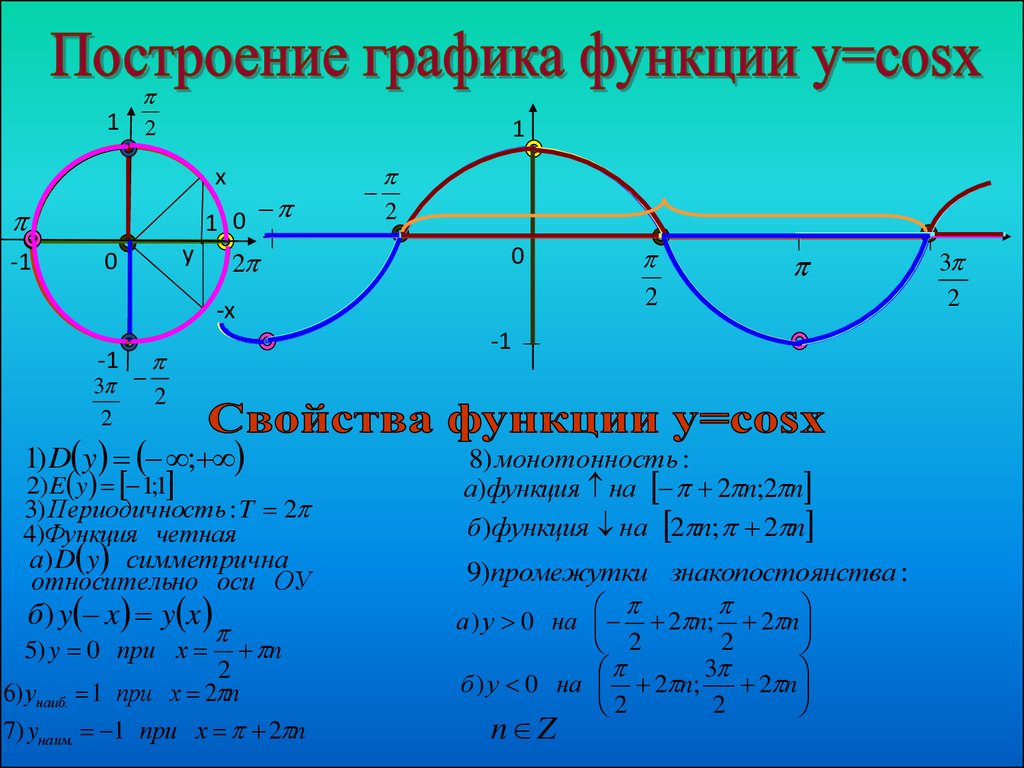
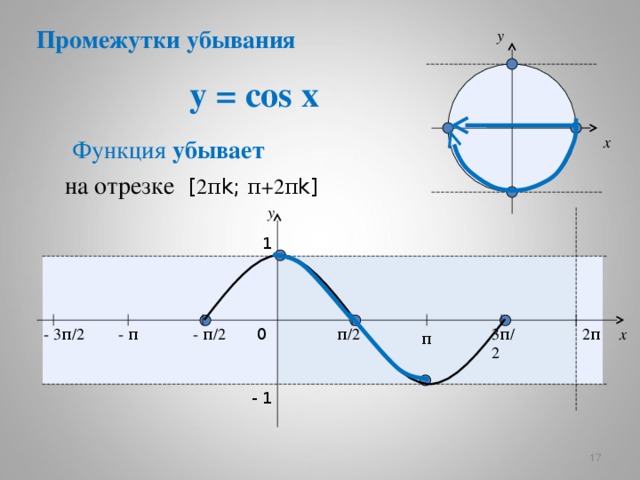
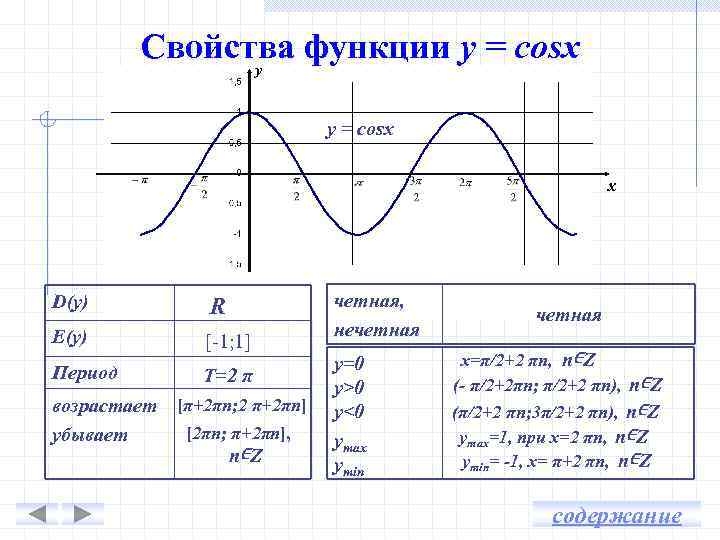
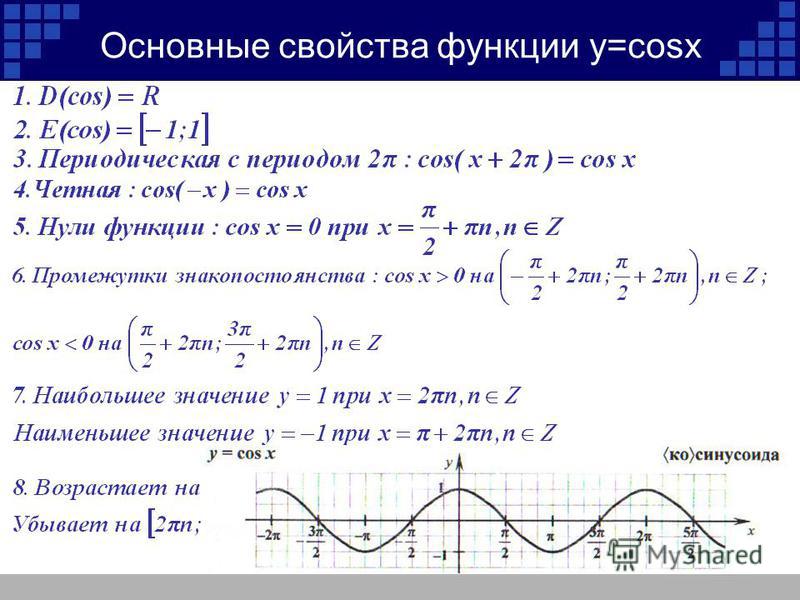
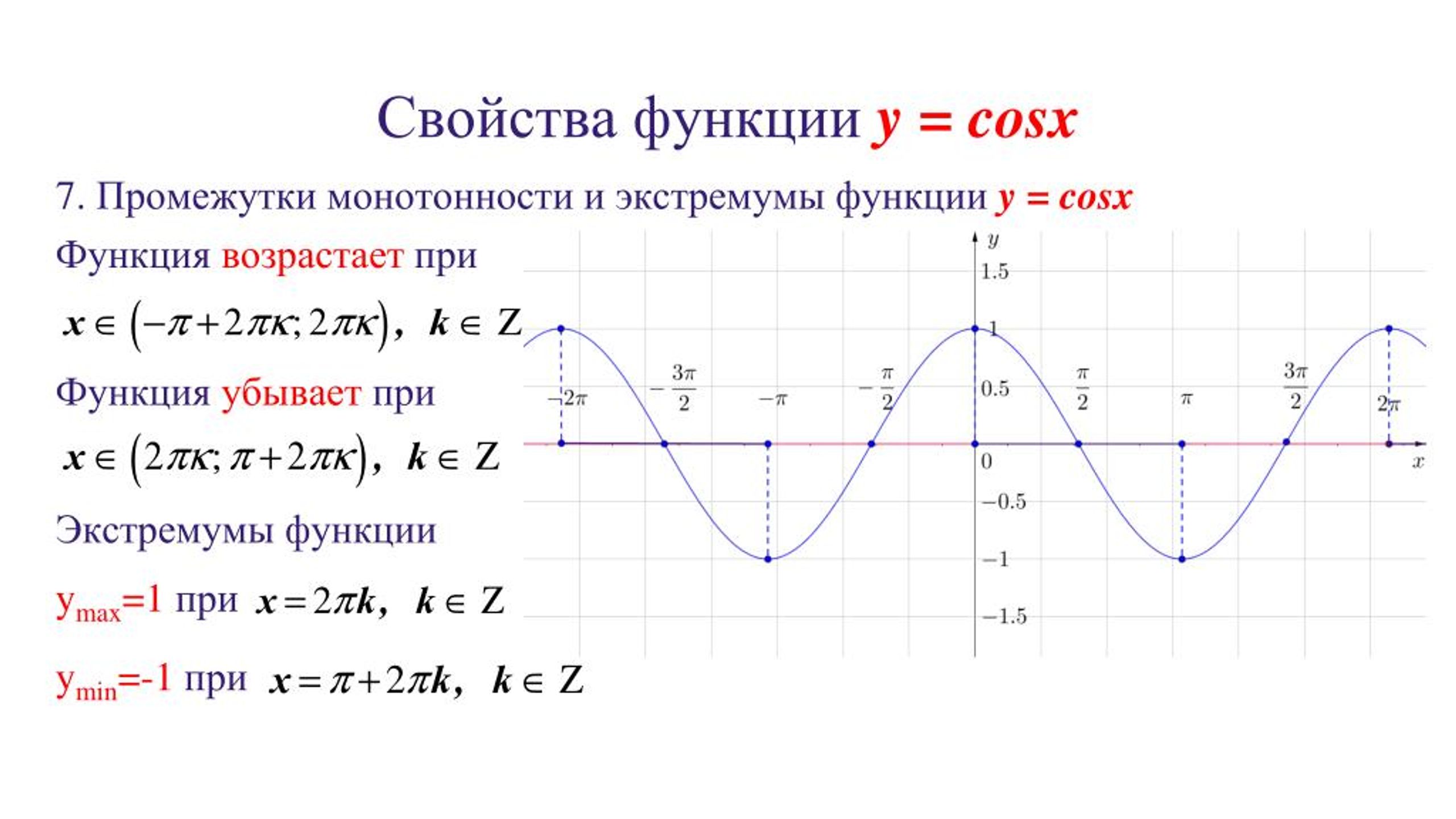
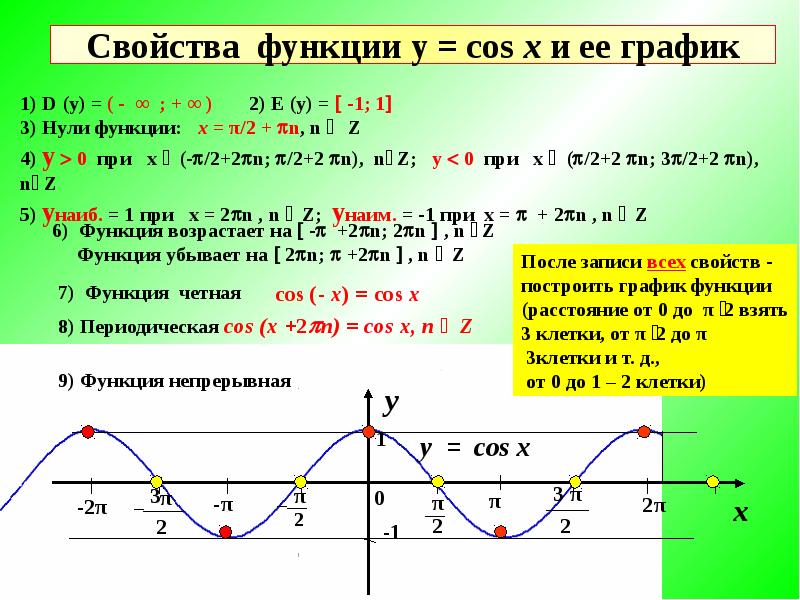
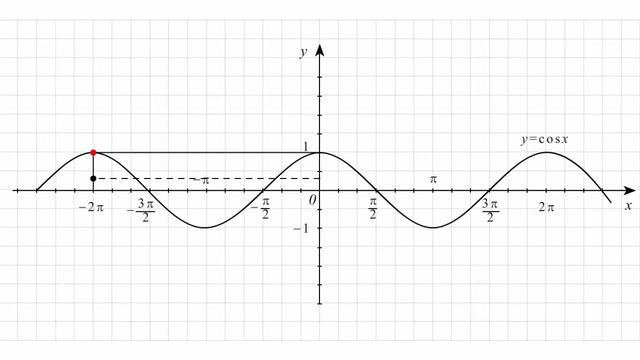 · Функция возрастает на промежутках и убывает на промежутках , . · Точки пересечения графика с осями: с осью О х , ; с осью Oy: y =0. · Интервалы знакопостоянства: при , ; y …
· Функция возрастает на промежутках и убывает на промежутках , . · Точки пересечения графика с осями: с осью О х , ; с осью Oy: y =0. · Интервалы знакопостоянства: при , ; y …
 Свойства и график функции y=Cosx. Теория и практика. Автор: Фадина Кристина Валерьевна. Соц.сети — ВК, Tg. Если нашли ошибку в тексте, выделите её и …
Свойства и график функции y=Cosx. Теория и практика. Автор: Фадина Кристина Валерьевна. Соц.сети — ВК, Tg. Если нашли ошибку в тексте, выделите её и …
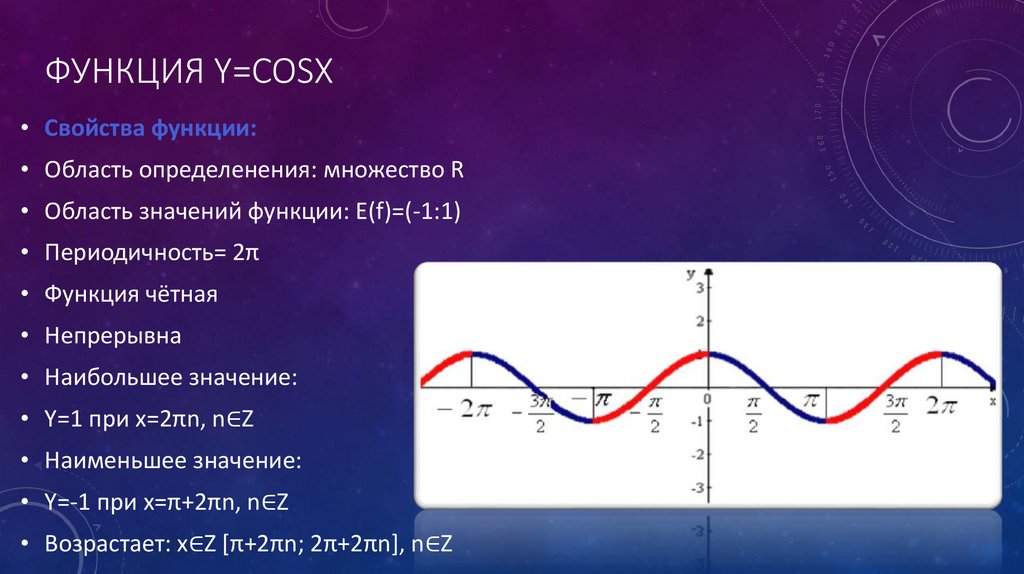 Функция y = cos (x) является тригонометрической функцией и имеет ряд свойств, которые помогают понять ее поведение и анализировать ее график. Одно из основных свойств …
Функция y = cos (x) является тригонометрической функцией и имеет ряд свойств, которые помогают понять ее поведение и анализировать ее график. Одно из основных свойств …
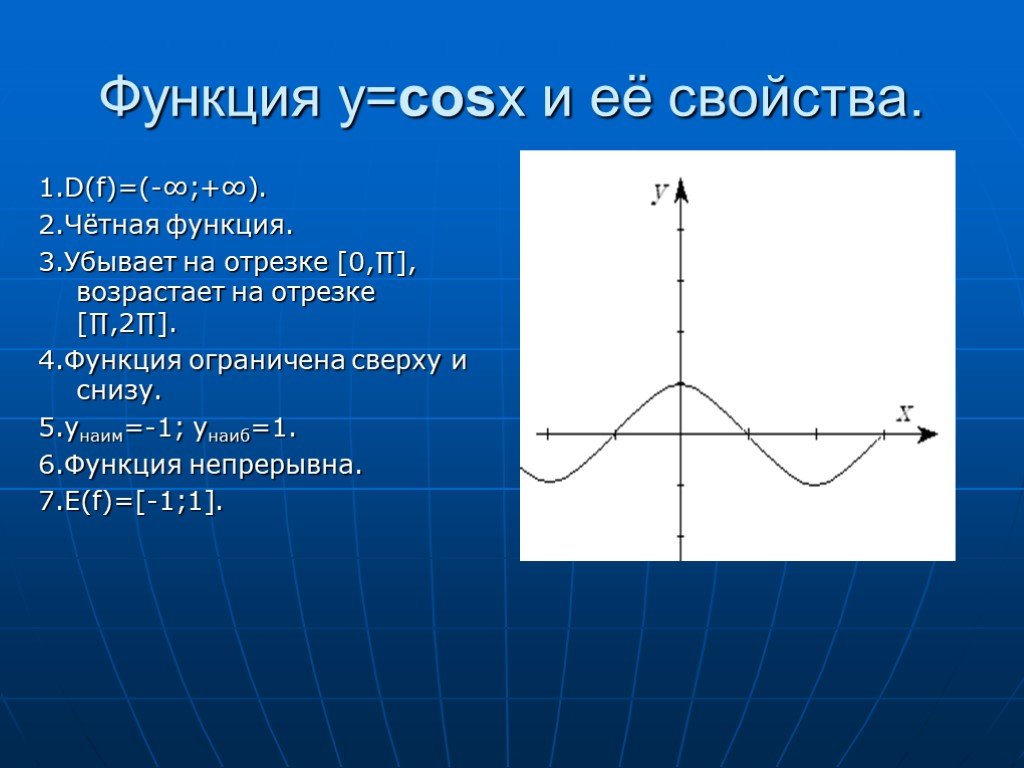
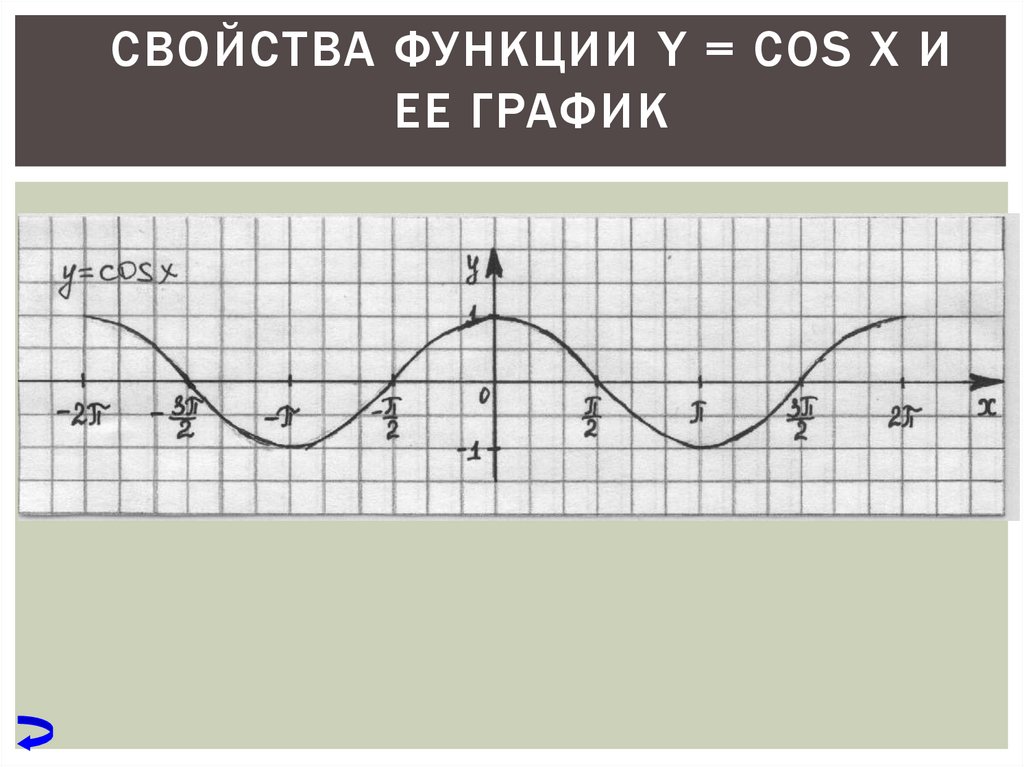 Свойства функции y=cosx. Область определения — D(f)=(-∞; +∞). Область значения — E(f)=[-1; 1]. Периодическая T=2π, непрерывная; Чётная, cos(-x)=cosx
Свойства функции y=cosx. Область определения — D(f)=(-∞; +∞). Область значения — E(f)=[-1; 1]. Периодическая T=2π, непрерывная; Чётная, cos(-x)=cosx
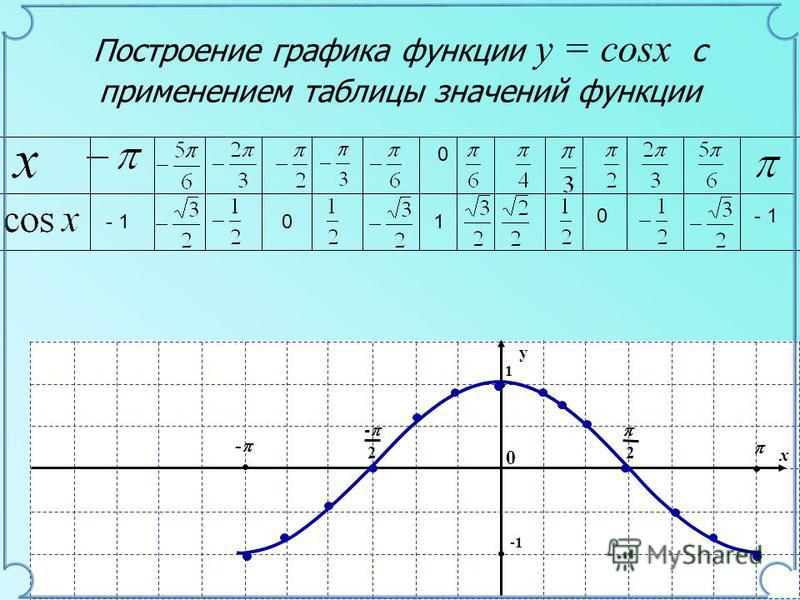
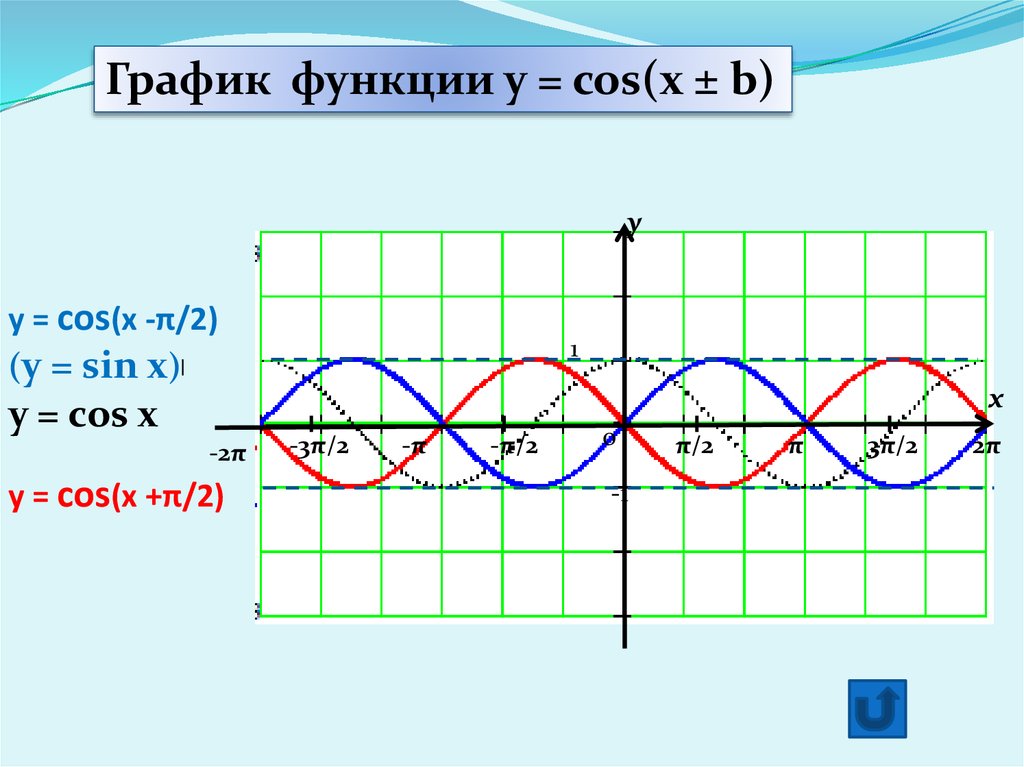
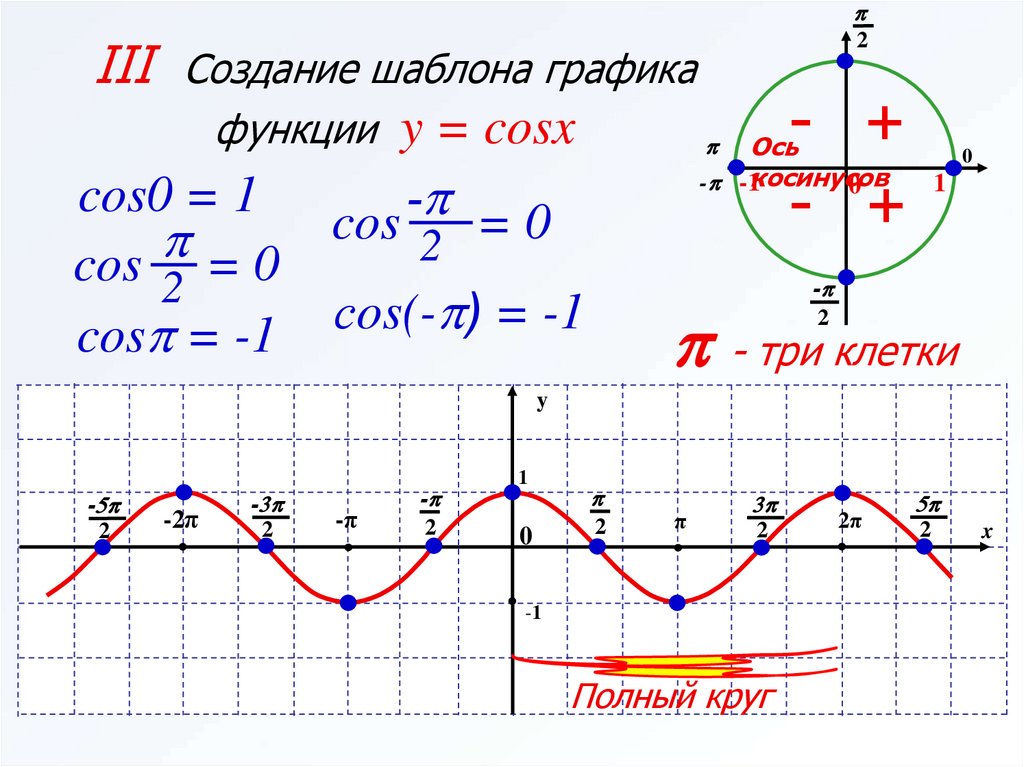
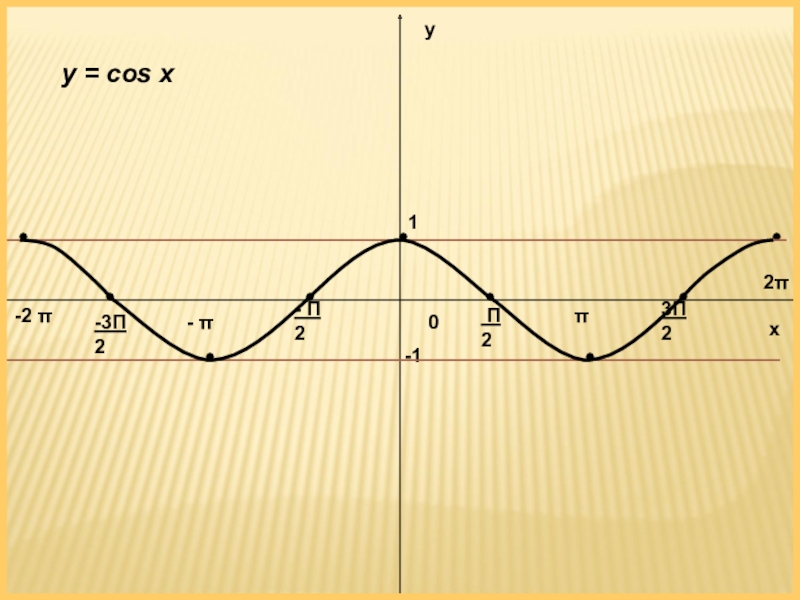
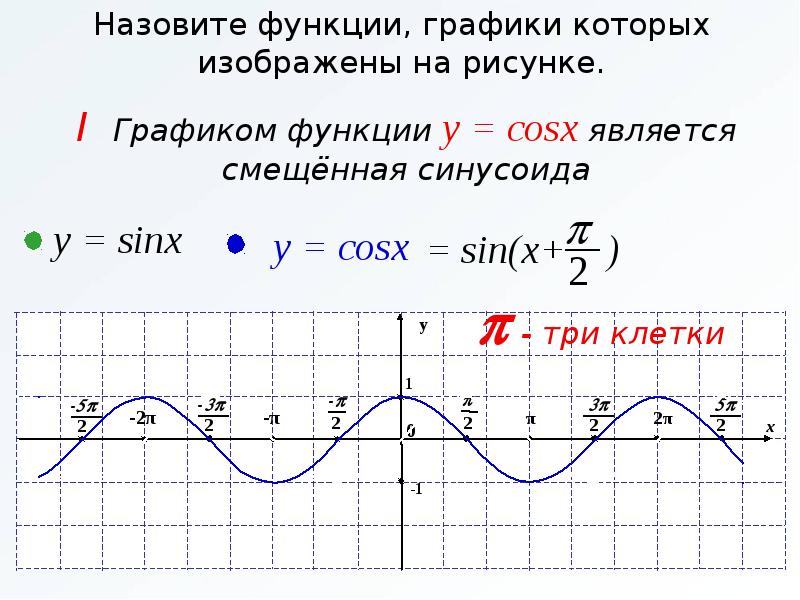
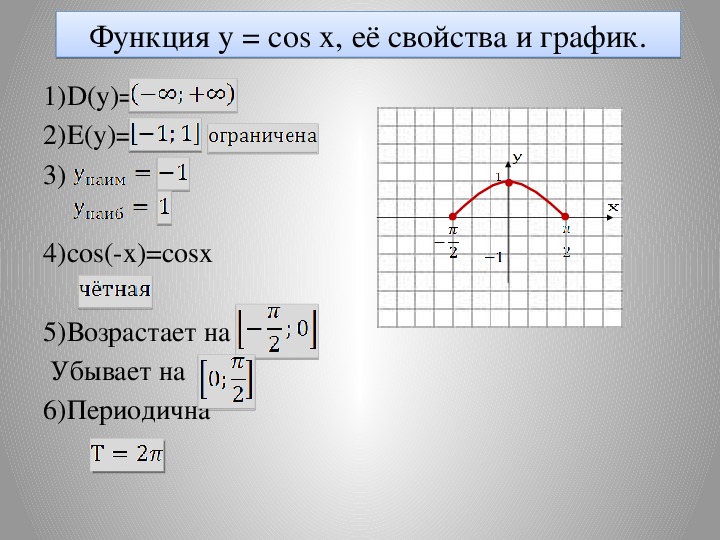 Построим функцию косинус на всей ее области определения. Для этого используем периодичности косинуса. Период функции y = cosx равен 2π.
Построим функцию косинус на всей ее области определения. Для этого используем периодичности косинуса. Период функции y = cosx равен 2π.
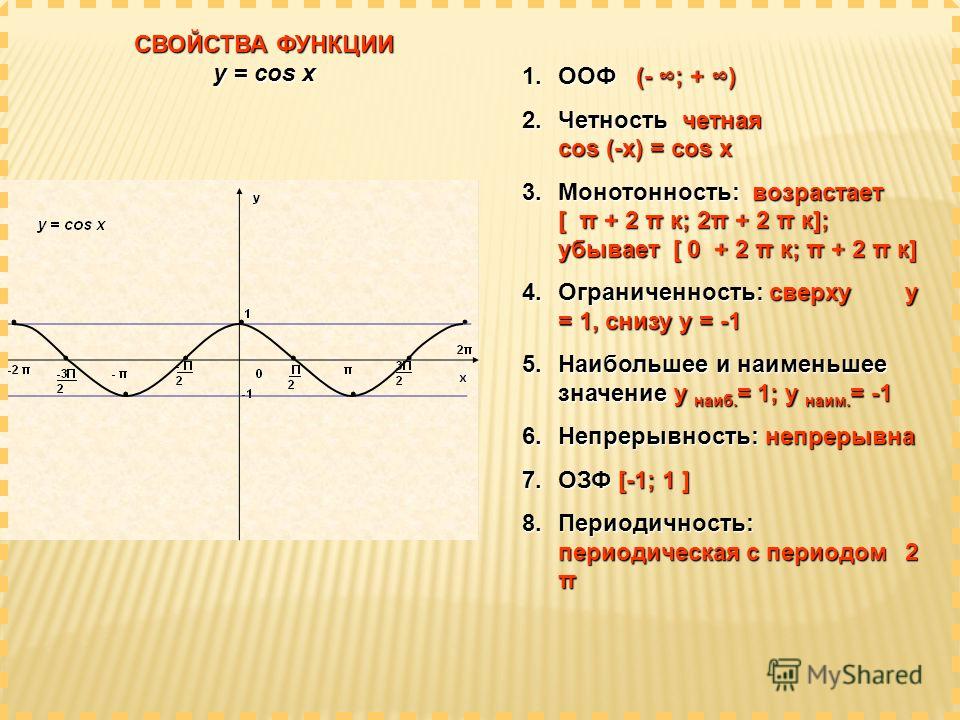 Функция косинус – это тригонометрическая функция от угла, который заключен между катетом и гипотенузой прямоугольного треугольника. График функции y = cos x …
Функция косинус – это тригонометрическая функция от угла, который заключен между катетом и гипотенузой прямоугольного треугольника. График функции y = cos x …
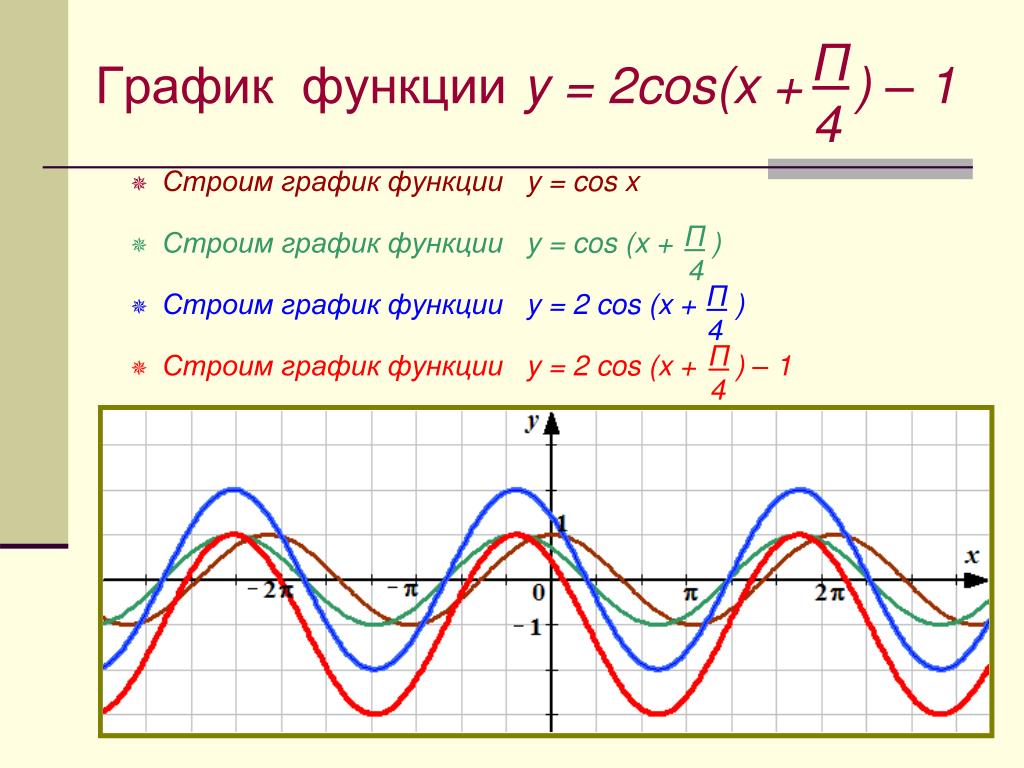
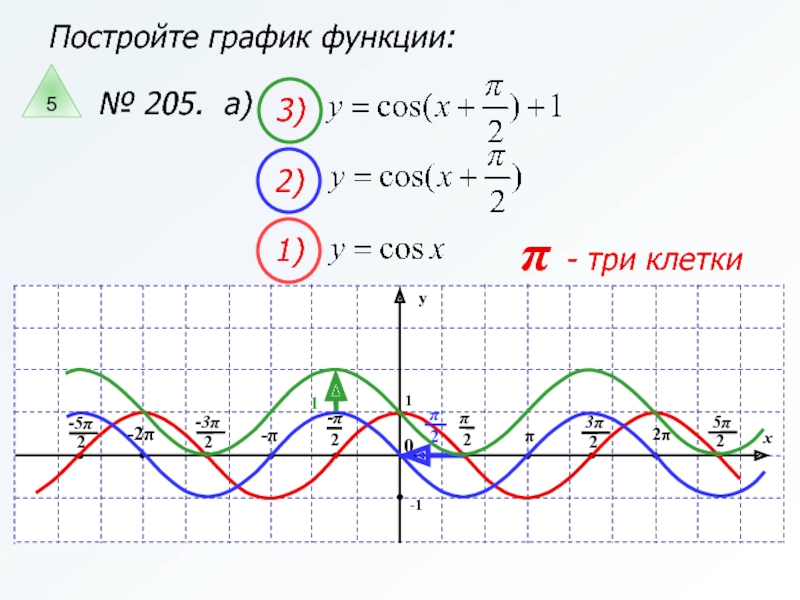
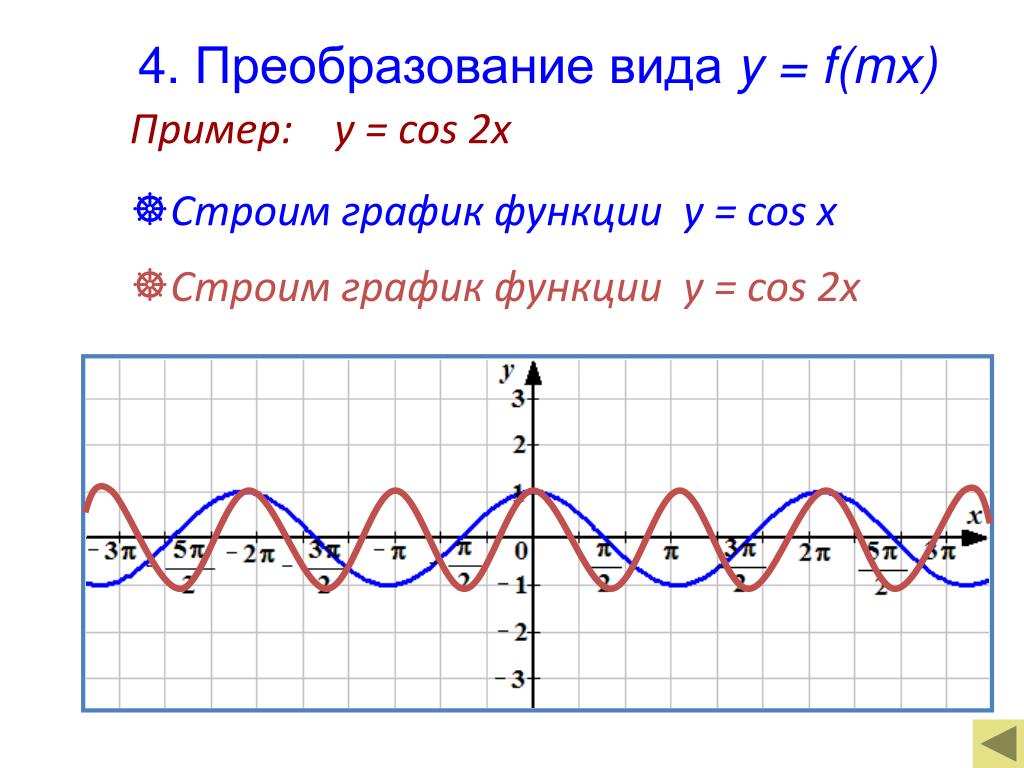
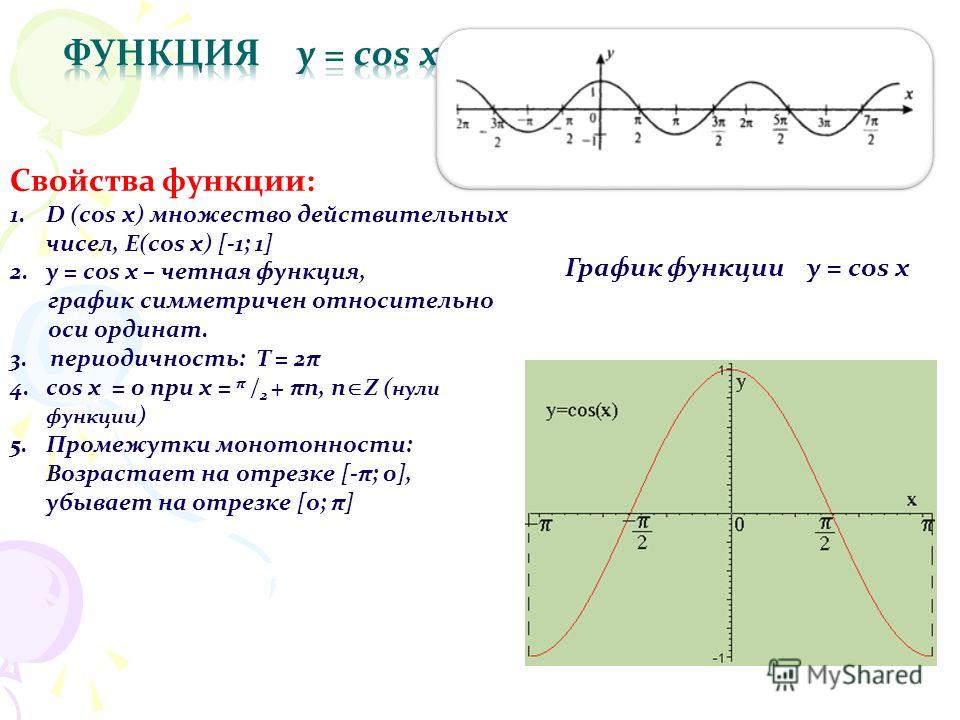 Обобщить преобразования графиков функций сдвигом по оси . Решить задания из №205 ( а, б ) и описать свойства функций.
Обобщить преобразования графиков функций сдвигом по оси . Решить задания из №205 ( а, б ) и описать свойства функций.
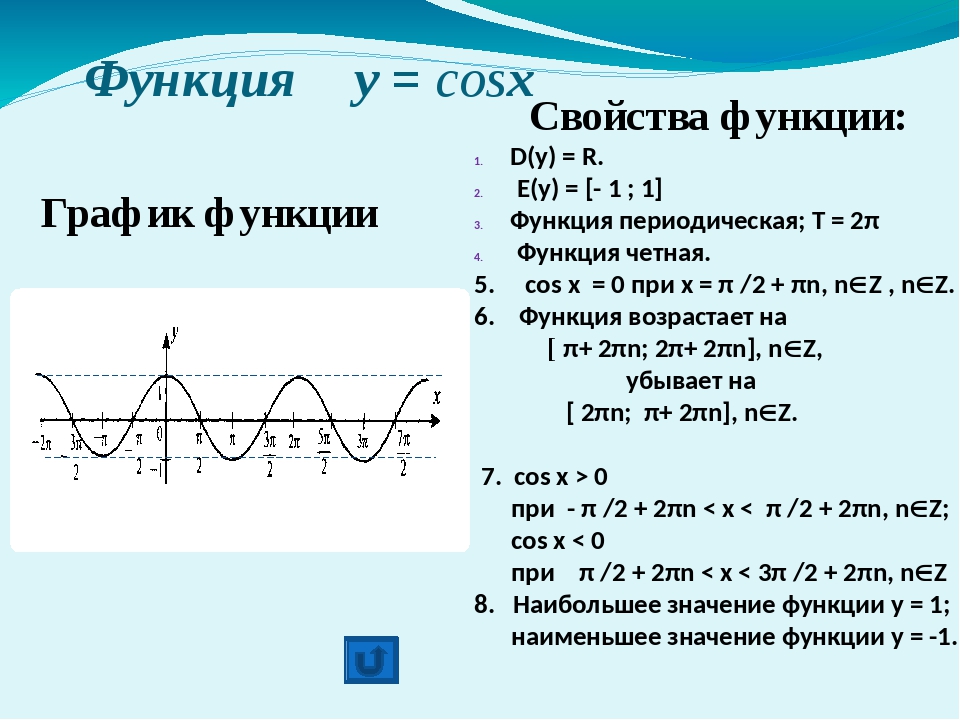 Функция $y=cosx$ – чётная, график симметричен относительно оси Оу. Какие ещё свойства есть у функции косинуса, присущие только ему?
Функция $y=cosx$ – чётная, график симметричен относительно оси Оу. Какие ещё свойства есть у функции косинуса, присущие только ему?
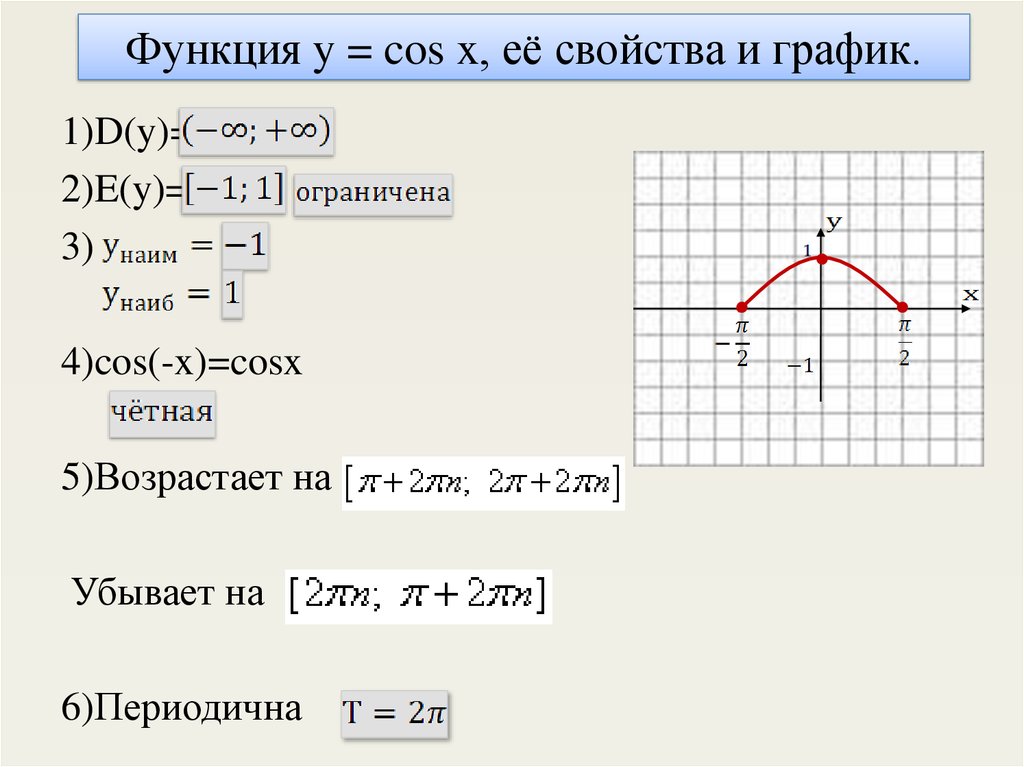 Функция y = cos x является тригонометрической функцией, где x представляет угол, а y - значение косинуса этого угла. Множество значений этой функции зависит от диапазона, …
Функция y = cos x является тригонометрической функцией, где x представляет угол, а y - значение косинуса этого угла. Множество значений этой функции зависит от диапазона, …
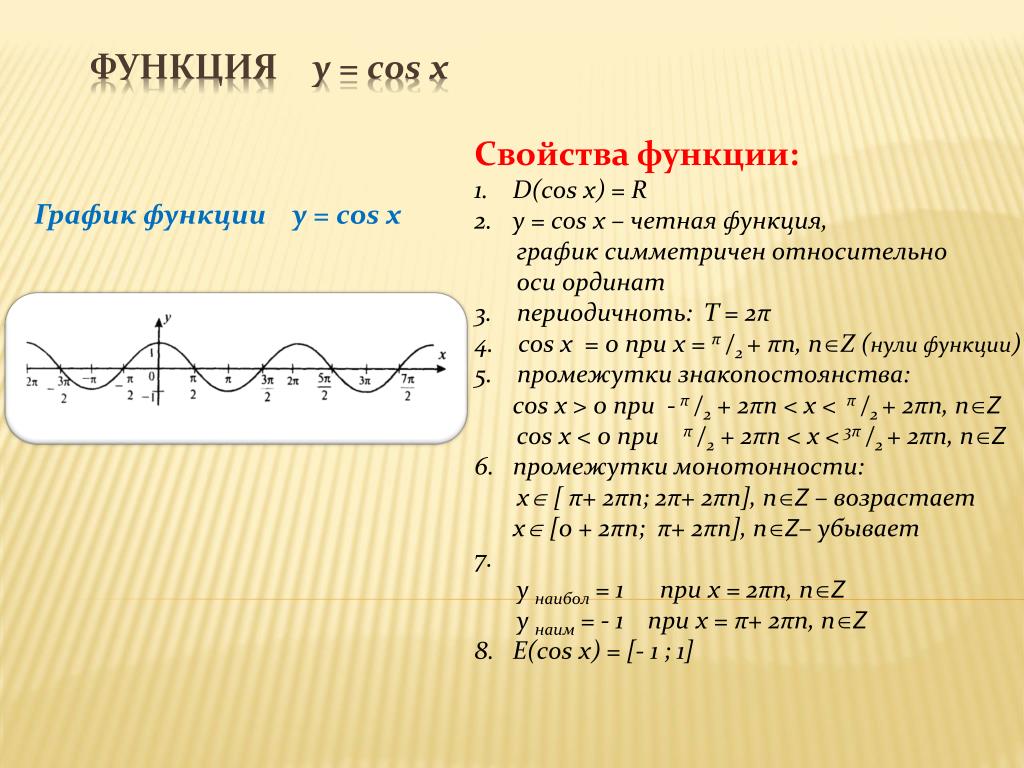 На этом уроке косинус рассматривается как функция аргумента x. Рассматриваются основные свойства функции y=cos x, строится график функции.
На этом уроке косинус рассматривается как функция аргумента x. Рассматриваются основные свойства функции y=cos x, строится график функции.
Еще по теме:



Еще по теме: